t-Exponential Memory Networks for Question-Answering Machines
Paper and Code
Sep 04, 2018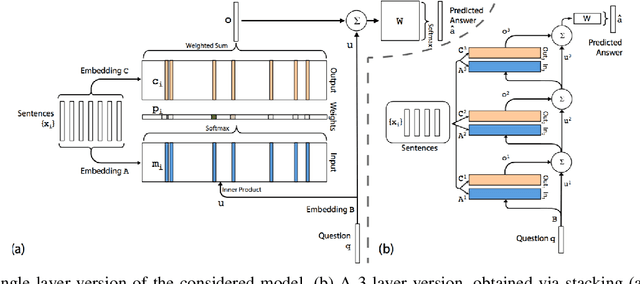
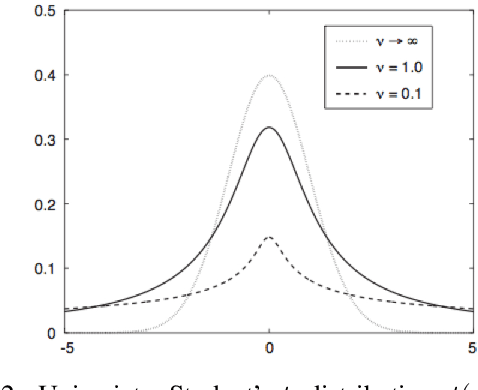
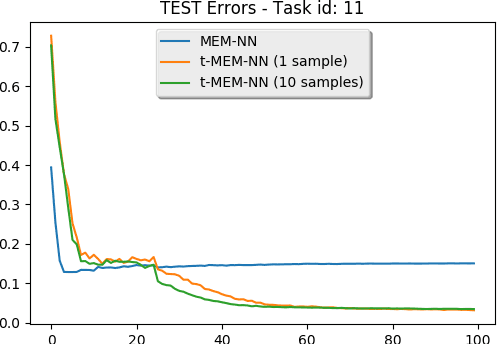

Recent advances in deep learning have brought to the fore models that can make multiple computational steps in the service of completing a task; these are capable of describ- ing long-term dependencies in sequential data. Novel recurrent attention models over possibly large external memory modules constitute the core mechanisms that enable these capabilities. Our work addresses learning subtler and more complex underlying temporal dynamics in language modeling tasks that deal with sparse sequential data. To this end, we improve upon these recent advances, by adopting concepts from the field of Bayesian statistics, namely variational inference. Our proposed approach consists in treating the network parameters as latent variables with a prior distribution imposed over them. Our statistical assumptions go beyond the standard practice of postulating Gaussian priors. Indeed, to allow for handling outliers, which are prevalent in long observed sequences of multivariate data, multivariate t-exponential distributions are imposed. On this basis, we proceed to infer corresponding posteriors; these can be used for inference and prediction at test time, in a way that accounts for the uncertainty in the available sparse training data. Specifically, to allow for our approach to best exploit the merits of the t-exponential family, our method considers a new t-divergence measure, which generalizes the concept of the Kullback-Leibler divergence. We perform an extensive experimental evaluation of our approach, using challenging language modeling benchmarks, and illustrate its superiority over existing state-of-the-art techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge