Symmetry & critical points for a model shallow neural network
Paper and Code
Mar 23, 2020
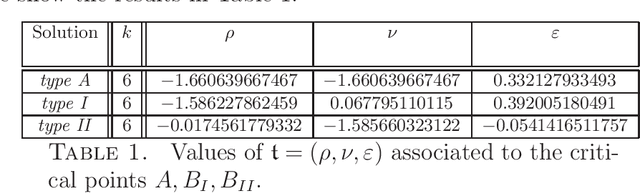

A detailed analysis is given of a family of critical points determining spurious minima for a model student-teacher 2-layer neural network, with ReLU activation function, and a natural $\Gamma = S_k \times S_k$-symmetry. For a $k$-neuron shallow network of this type, analytic equations are given which, for example, determine the critical points of the spurious minima described by Safran and Shamir (2018) for $6 \le k \le 20$. These critical points have isotropy (conjugate to) the diagonal subgroup $\Delta S_{k-1}\subset \Delta S_k$ of $\Gamma$. It is shown that critical points of this family can be expressed as an infinite series in $1/\sqrt{k}$ (for large enough $k$) and, as an application, the critical values decay like $a k^{-1}$, where $a \approx 0.3$. Other non-trivial families of critical points are also described with isotropy conjugate to $\Delta S_{k-1}, \Delta S_k$ and $\Delta (S_2\times S_{k-2})$ (the latter giving spurious minima for $k\ge 9$). The methods used depend on symmetry breaking, bifurcation, and algebraic geometry, notably Artin's implicit function theorem, and are applicable to other families of critical points that occur in this network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge