Symmetry Breaking in Neuroevolution: A Technical Report
Paper and Code
Jul 22, 2011
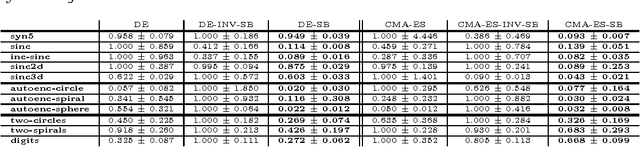
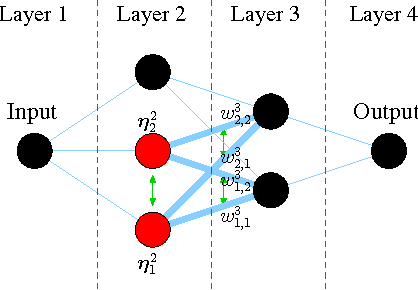
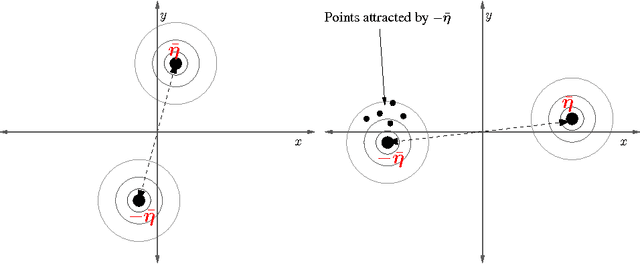
Artificial Neural Networks (ANN) comprise important symmetry properties, which can influence the performance of Monte Carlo methods in Neuroevolution. The problem of the symmetries is also known as the competing conventions problem or simply as the permutation problem. In the literature, symmetries are mainly addressed in Genetic Algoritm based approaches. However, investigations in this direction based on other Evolutionary Algorithms (EA) are rare or missing. Furthermore, there are different and contradictionary reports on the efficacy of symmetry breaking. By using a novel viewpoint, we offer a possible explanation for this issue. As a result, we show that a strategy which is invariant to the global optimum can only be successfull on certain problems, whereas it must fail to improve the global convergence on others. We introduce the \emph{Minimum Global Optimum Proximity} principle as a generalized and adaptive strategy to symmetry breaking, which depends on the location of the global optimum. We apply the proposed principle to Differential Evolution (DE) and Covariance Matrix Adaptation Evolution Strategies (CMA-ES), which are two popular and conceptually different global optimization methods. Using a wide range of feedforward ANN problems, we experimentally illustrate significant improvements in the global search efficiency by the proposed symmetry breaking technique.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge