Switch Spaces: Learning Product Spaces with Sparse Gating
Paper and Code
Feb 17, 2021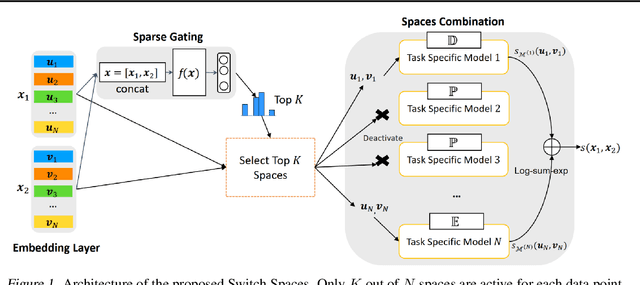
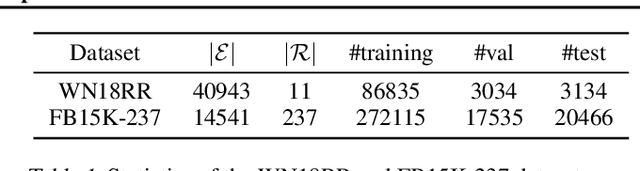
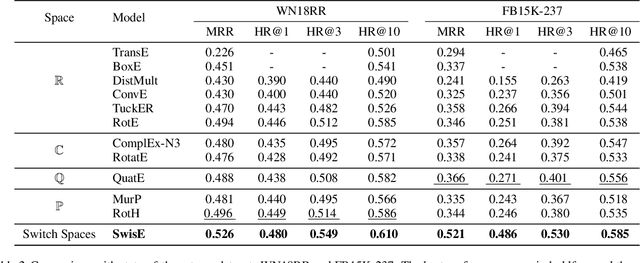
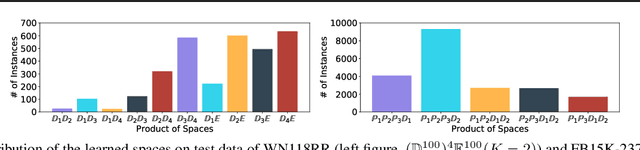
Learning embedding spaces of suitable geometry is critical for representation learning. In order for learned representations to be effective and efficient, it is ideal that the geometric inductive bias aligns well with the underlying structure of the data. In this paper, we propose Switch Spaces, a data-driven approach for learning representations in product space. Specifically, product spaces (or manifolds) are spaces of mixed curvature, i.e., a combination of multiple euclidean and non-euclidean (hyperbolic, spherical) manifolds. To this end, we introduce sparse gating mechanisms that learn to choose, combine and switch spaces, allowing them to be switchable depending on the input data with specialization. Additionally, the proposed method is also efficient and has a constant computational complexity regardless of the model size. Experiments on knowledge graph completion and item recommendations show that the proposed switch space achieves new state-of-the-art performances, outperforming pure product spaces and recently proposed task-specific models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge