Supervised Community Detection with Line Graph Neural Networks

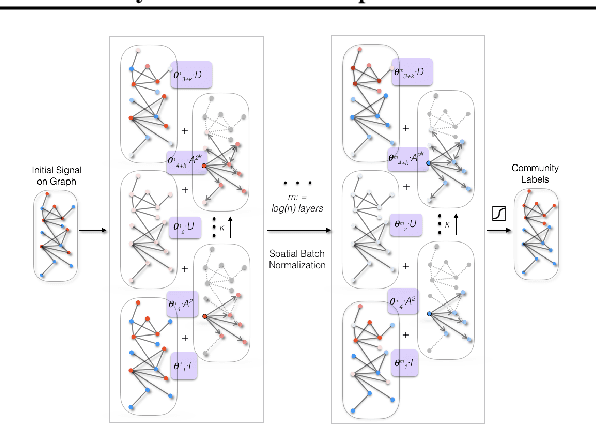
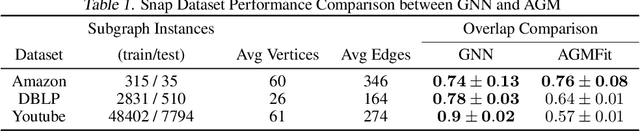
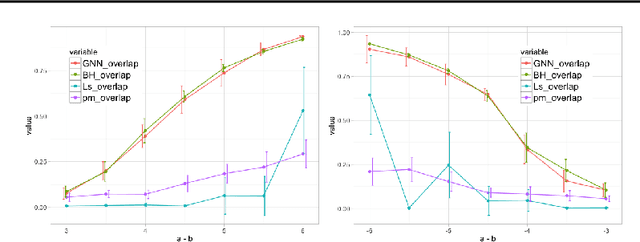
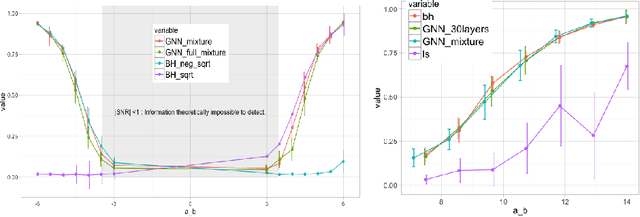
We study data-driven methods for community detection on graphs, an inverse problem that is typically solved in terms of the spectrum of certain operators or via posterior inference under certain probabilistic graphical models. Focusing on random graph families such as the stochastic block model, recent research has unified both approaches and identified both statistical and computational signal-to-noise detection thresholds. This graph inference task can be recast as a node-wise graph classification problem, and, as such, computational detection thresholds can be translated in terms of learning within appropriate models. We present a novel family of Graph Neural Networks (GNNs) and show that they can reach those detection thresholds in a purely data-driven manner without access to the underlying generative models, and even improve upon current computational thresholds in hard regimes. For that purpose, we propose to augment GNNs with the non-backtracking operator, defined on the line graph of edge adjacencies. We also perform the first analysis of optimization landscape on using GNNs to solve community detection problems, demonstrating that under certain simplifications and assumptions, the loss value at the local minima is close to the loss value at the global minimum/minima. Finally, the resulting model is also tested on real datasets, performing significantly better than previous models.