Subspace Networks for Few-shot Classification

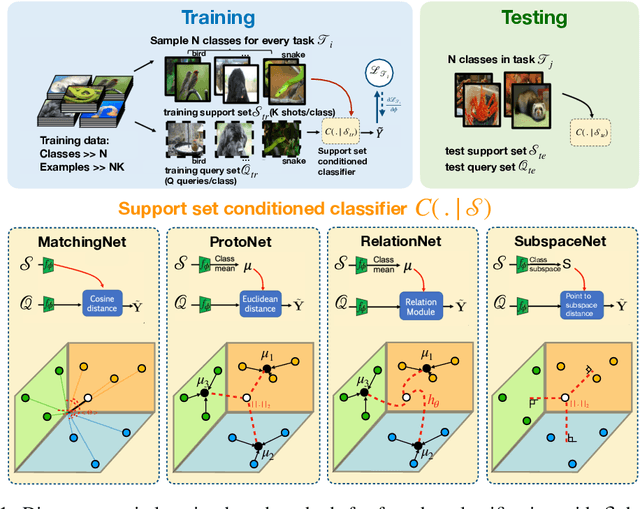
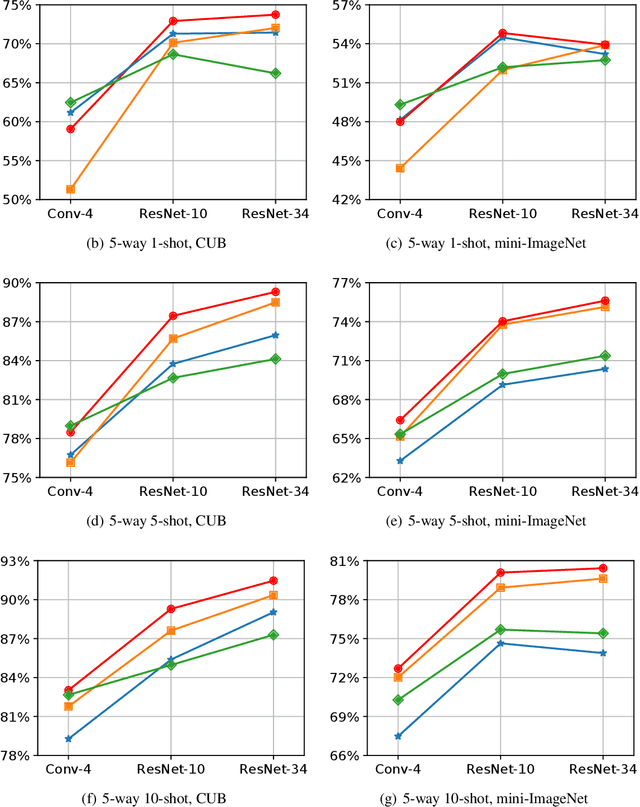
We propose subspace networks for the problem of few-shot classification, where a classifier must generalize to new classes not seen in the training set, given only a small number of examples of each class. Subspace networks learn an embedding space in which classification can be performed by computing distances of embedded points to subspace representations of each class. The class subspaces are spanned by examples belonging to the same class, transformed by a learnable embedding function. Similarly to recent approaches for few-shot learning, subspace networks reflect a simple inductive bias that is beneficial in this limited-data regime and they achieve excellent results. In particular, our proposed method shows consistently better performance than other state-of-the-art few-shot distance-metric learning methods when the embedding function is deep or when training and testing domains are shifted.