Sub-Block Rearranged Staircase Codes for Optical Transport Networks
Paper and Code
Jun 28, 2022
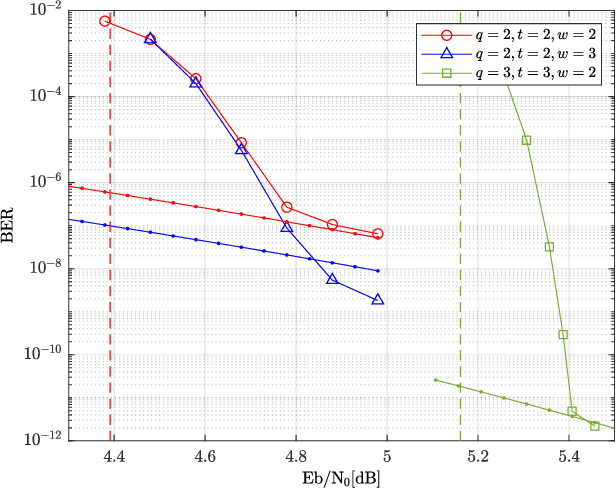

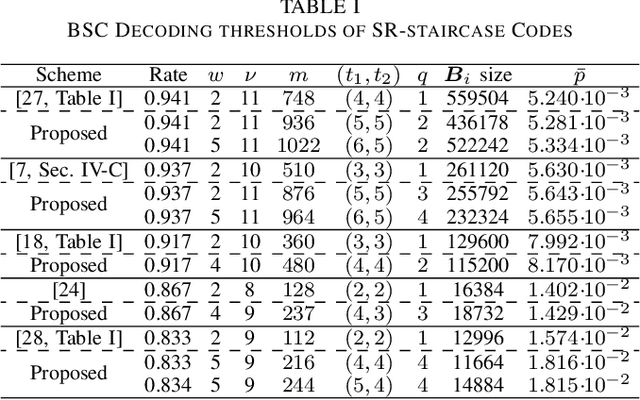
We propose a new family of spatially coupled product codes, called sub-block rearranged staircase (SR-staircase) codes. Each SR-staircase code block is constructed by encoding rearranged preceding code blocks and new information blocks, where the rearrangement involves sub-blocks decomposition and transposition. The proposed codes can be constructed to have each code block size of $1/q$ to that of the conventional staircase codes while having the same rate and component codes, for any positive integer $q$. In this regard, we can use strong algebraic component codes to construct SR-staircase codes with a similar or the same code block size and rate as staircase codes with weak component codes. Moreover, both waterfall and error floor performance can be further improved by using a large coupling width. The superior performance of the proposed codes is demonstrated through density evolution and error floor analysis as well as simulation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge