Structured Covariance Matrix Estimation with Missing-Data for Radar Applications via Expectation-Maximization
Paper and Code
May 08, 2021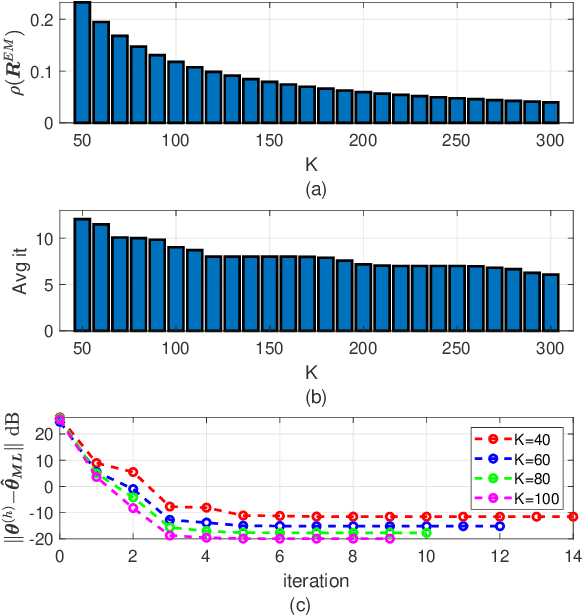
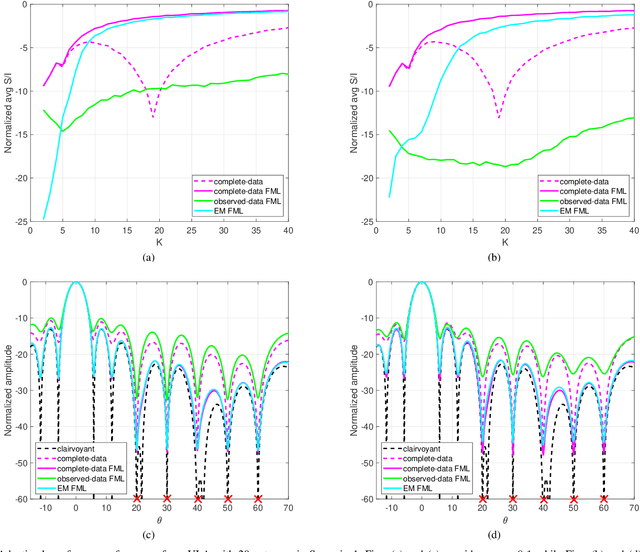

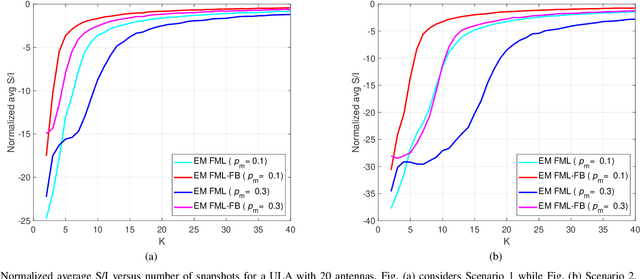
Structured covariance matrix estimation in the presence of missing data is addressed in this paper with emphasis on radar signal processing applications. After a motivation of the study, the array model is specified and the problem of computing the maximum likelihood estimate of a structured covariance matrix is formulated. A general procedure to optimize the observed-data likelihood function is developed resorting to the expectation-maximization algorithm. The corresponding convergence properties are thoroughly established and the rate of convergence is analyzed. The estimation technique is contextualized for two practically relevant radar problems: beamforming and detection of the number of sources. In the former case an adaptive beamformer leveraging the EM-based estimator is presented; in the latter, detection techniques generalizing the classic Akaike information criterion, minimum description length, and Hannan-Quinn information criterion, are introduced. Numerical results are finally presented to corroborate the theoretical study.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge