Structure Learning of Quantum Embeddings
Paper and Code
Sep 22, 2022

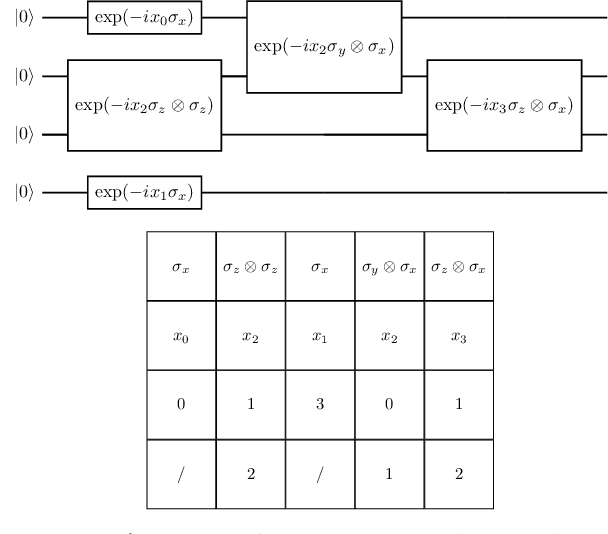

The representation of data is of paramount importance for machine learning methods. Kernel methods are used to enrich the feature representation, allowing better generalization. Quantum kernels implement efficiently complex transformation encoding classical data in the Hilbert space of a quantum system, resulting in even exponential speedup. However, we need prior knowledge of the data to choose an appropriate parametric quantum circuit that can be used as quantum embedding. We propose an algorithm that automatically selects the best quantum embedding through a combinatorial optimization procedure that modifies the structure of the circuit, changing the generators of the gates, their angles (which depend on the data points), and the qubits on which the various gates act. Since combinatorial optimization is computationally expensive, we have introduced a criterion based on the exponential concentration of kernel matrix coefficients around the mean to immediately discard an arbitrarily large portion of solutions that are believed to perform poorly. Contrary to the gradient-based optimization (e.g. trainable quantum kernels), our approach is not affected by the barren plateau by construction. We have used both artificial and real-world datasets to demonstrate the increased performance of our approach with respect to randomly generated PQC. We have also compared the effect of different optimization algorithms, including greedy local search, simulated annealing, and genetic algorithms, showing that the algorithm choice largely affects the result.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge