Struct-MMSB: Mixed Membership Stochastic Blockmodels with Interpretable Structured Priors
Paper and Code
Feb 21, 2020
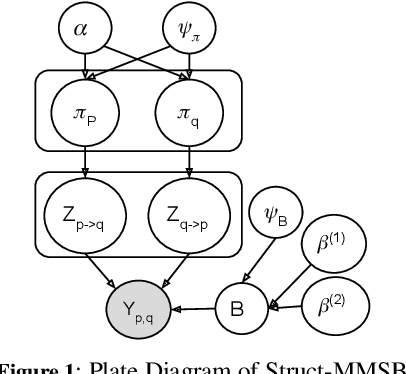
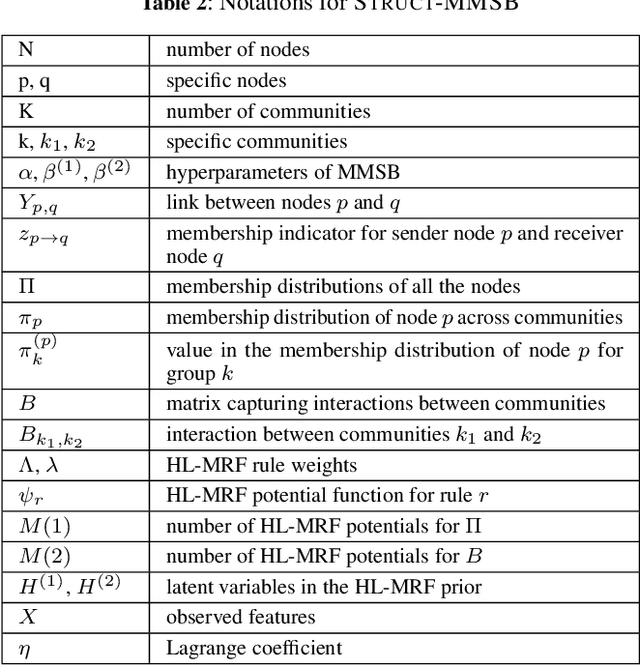
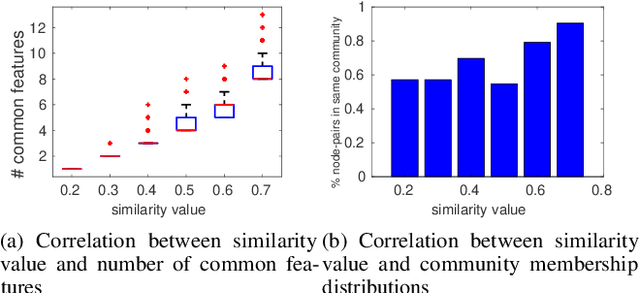
The mixed membership stochastic blockmodel (MMSB) is a popular framework for community detection and network generation. It learns a low-rank mixed membership representation for each node across communities by exploiting the underlying graph structure. MMSB assumes that the membership distributions of the nodes are independently drawn from a Dirichlet distribution, which limits its capability to model highly correlated graph structures that exist in real-world networks. In this paper, we present a flexible richly structured MMSB model, \textit{Struct-MMSB}, that uses a recently developed statistical relational learning model, hinge-loss Markov random fields (HL-MRFs), as a structured prior to model complex dependencies among node attributes, multi-relational links, and their relationship with mixed-membership distributions. Our model is specified using a probabilistic programming templating language that uses weighted first-order logic rules, which enhances the model's interpretability. Further, our model is capable of learning latent characteristics in real-world networks via meaningful latent variables encoded as a complex combination of observed features and membership distributions. We present an expectation-maximization based inference algorithm that learns latent variables and parameters iteratively, a scalable stochastic variation of the inference algorithm, and a method to learn the weights of HL-MRF structured priors. We evaluate our model on six datasets across three different types of networks and corresponding modeling scenarios and demonstrate that our models are able to achieve an improvement of 15\% on average in test log-likelihood and faster convergence when compared to state-of-the-art network models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge