Stochastic Smoothing for Nonsmooth Minimizations: Accelerating SGD by Exploiting Structure
Paper and Code
Oct 01, 2012


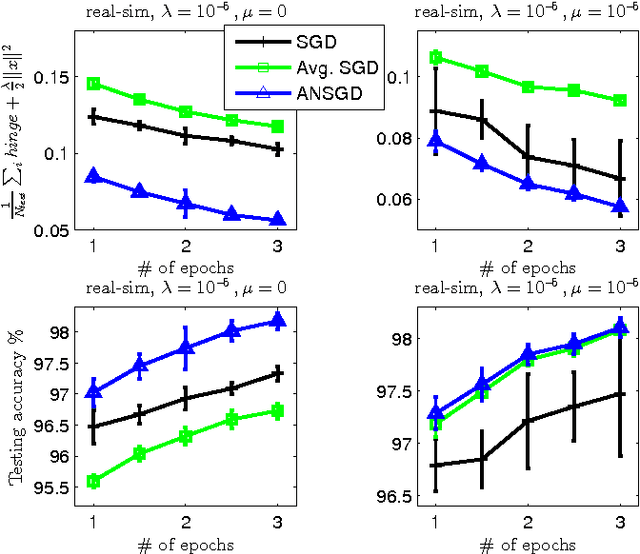
In this work we consider the stochastic minimization of nonsmooth convex loss functions, a central problem in machine learning. We propose a novel algorithm called Accelerated Nonsmooth Stochastic Gradient Descent (ANSGD), which exploits the structure of common nonsmooth loss functions to achieve optimal convergence rates for a class of problems including SVMs. It is the first stochastic algorithm that can achieve the optimal O(1/t) rate for minimizing nonsmooth loss functions (with strong convexity). The fast rates are confirmed by empirical comparisons, in which ANSGD significantly outperforms previous subgradient descent algorithms including SGD.
* Full length version of ICML'12 with all proofs. In this version, a
bug in proving Theorem 6 is fixed. We'd like to thank Dr. Francesco Orabona
for pointing it out
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge