Stochastic Online Convex Optimization; Application to probabilistic time series forecasting
Paper and Code
Feb 01, 2021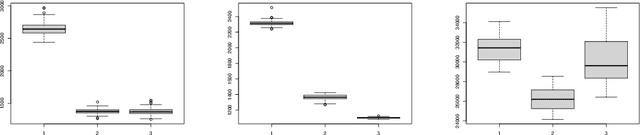
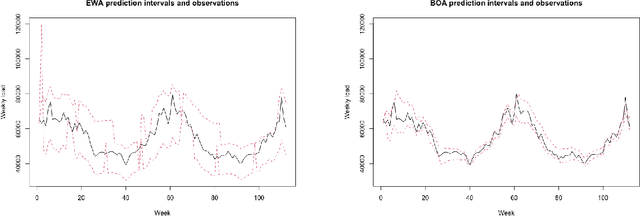
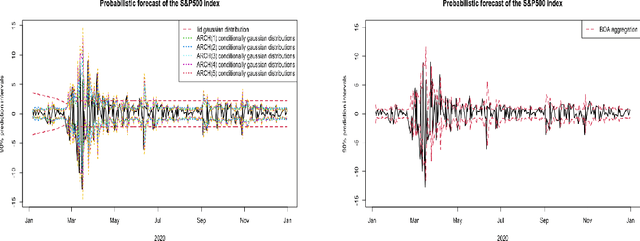
Stochastic regret bounds for online algorithms are usually derived from an "online to batch" conversion. Inverting the reasoning, we start our analyze by a "batch to online" conversion that applies in any Stochastic Online Convex Optimization problem under stochastic exp-concavity condition. We obtain fast rate stochastic regret bounds with high probability for non-convex loss functions. Based on this approach, we provide prediction and probabilistic forecasting methods for non-stationary unbounded time series.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge