Stochastic Nonlinear Control via Finite-dimensional Spectral Dynamic Embedding

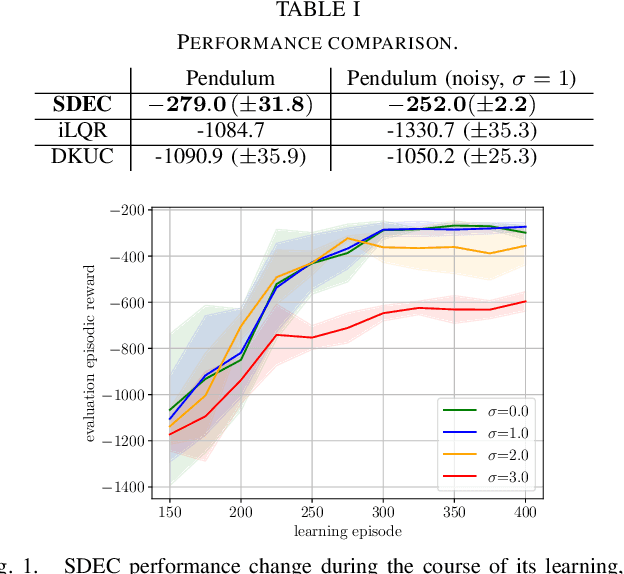
Optimal control is notoriously difficult for stochastic nonlinear systems. Ren et al. introduced Spectral Dynamics Embedding for developing reinforcement learning methods for controlling an unknown system. It uses an infinite-dimensional feature to linearly represent the state-value function and exploits finite-dimensional truncation approximation for practical implementation. However, the finite-dimensional approximation properties in control have not been investigated even when the model is known. In this paper, we provide a tractable stochastic nonlinear control algorithm that exploits the nonlinear dynamics upon the finite-dimensional feature approximation, Spectral Dynamics Embedding Control (SDEC), with an in-depth theoretical analysis to characterize the approximation error induced by the finite-dimension truncation and statistical error induced by finite-sample approximation in both policy evaluation and policy optimization. We also empirically test the algorithm and compare the performance with Koopman-based methods and iLQR methods on the pendulum swingup problem.