Stochastic Feedforward Neural Networks: Universal Approximation
Paper and Code
Oct 22, 2019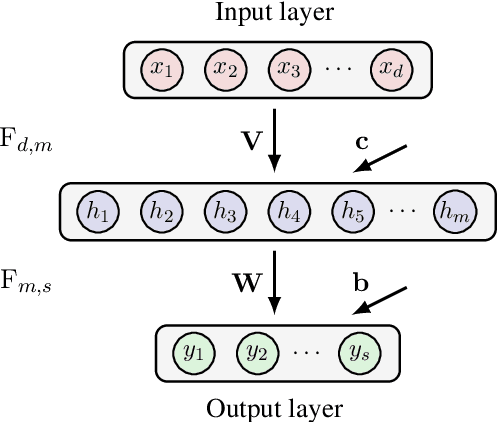
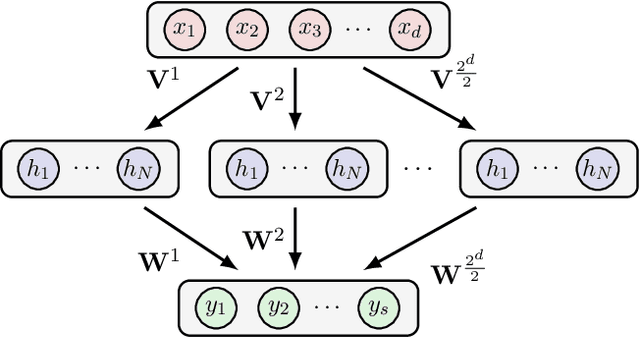
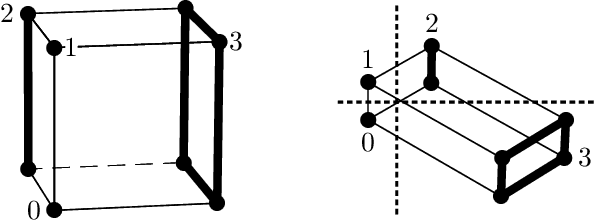
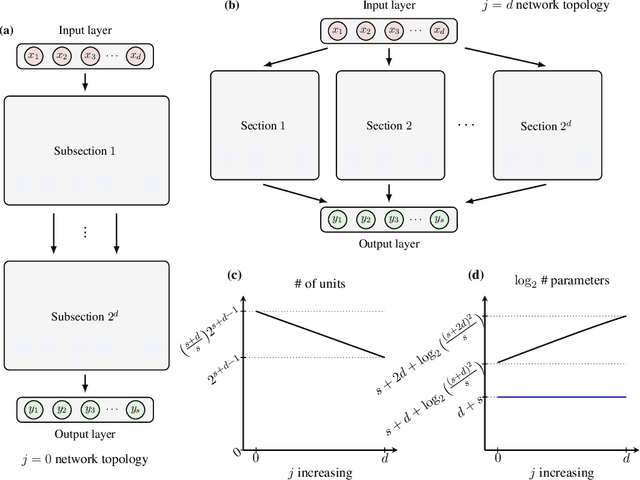
In this chapter we take a look at the universal approximation question for stochastic feedforward neural networks. In contrast to deterministic networks, which represent mappings from a set of inputs to a set of outputs, stochastic networks represent mappings from a set of inputs to a set of probability distributions over the set of outputs. In particular, even if the sets of inputs and outputs are finite, the class of stochastic mappings in question is not finite. Moreover, while for a deterministic function the values of all output variables can be computed independently of each other given the values of the inputs, in the stochastic setting the values of the output variables may need to be correlated, which requires that their values are computed jointly. A prominent class of stochastic feedforward networks which has played a key role in the resurgence of deep learning are deep belief networks. The representational power of these networks has been studied mainly in the generative setting, as models of probability distributions without an input, or in the discriminative setting for the special case of deterministic mappings. We study the representational power of deep sigmoid belief networks in terms of compositions of linear transformations of probability distributions, Markov kernels, that can be expressed by the layers of the network. We investigate different types of shallow and deep architectures, and the minimal number of layers and units per layer that are sufficient and necessary in order for the network to be able to approximate any given stochastic mapping from the set of inputs to the set of outputs arbitrarily well.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge