STL: A Signed and Truncated Logarithm Activation Function for Neural Networks
Paper and Code
Jul 31, 2023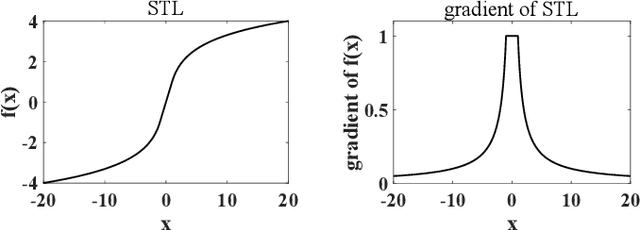
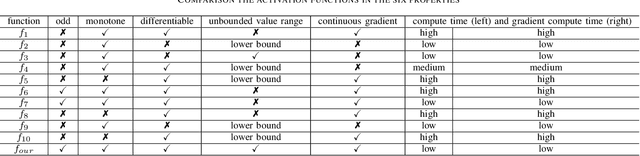
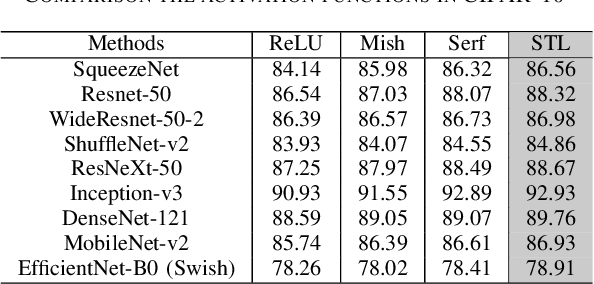
Activation functions play an essential role in neural networks. They provide the non-linearity for the networks. Therefore, their properties are important for neural networks' accuracy and running performance. In this paper, we present a novel signed and truncated logarithm function as activation function. The proposed activation function has significantly better mathematical properties, such as being odd function, monotone, differentiable, having unbounded value range, and a continuous nonzero gradient. These properties make it an excellent choice as an activation function. We compare it with other well-known activation functions in several well-known neural networks. The results confirm that it is the state-of-the-art. The suggested activation function can be applied in a large range of neural networks where activation functions are necessary.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge