Stiffness: A New Perspective on Generalization in Neural Networks

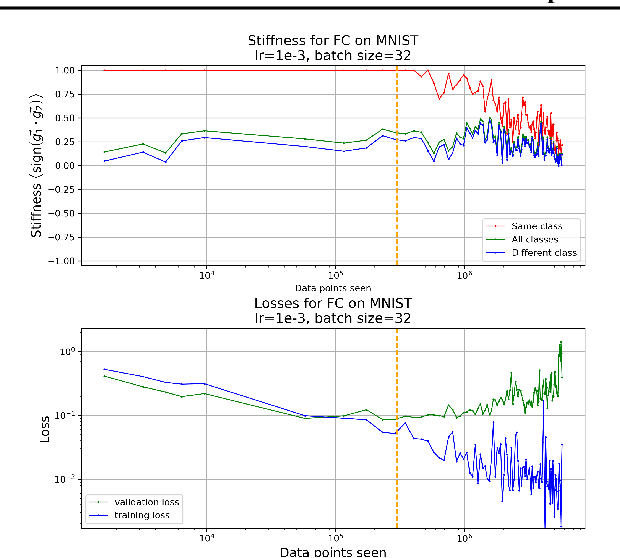
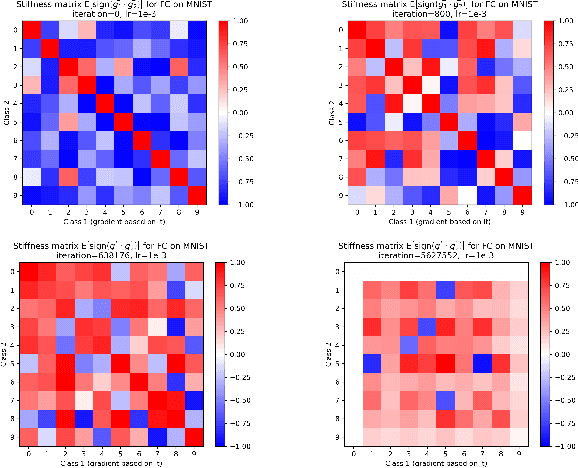
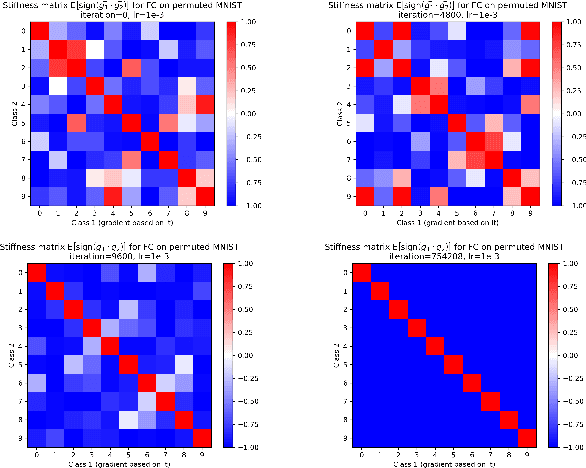
We investigate neural network training and generalization using the concept of stiffness. We measure how stiff a network is by looking at how a small gradient step on one example affects the loss on another example. In particular, we study how stiffness varies with 1) class membership, 2) distance between data points (in the input space as well as in latent spaces), 3) training iteration, and 4) learning rate. We empirically study the evolution of stiffness on MNIST, FASHION MNIST, CIFAR-10 and CIFAR-100 using fully-connected and convolutional neural networks. Our results demonstrate that stiffness is a useful concept for diagnosing and characterizing generalization. We observe that small learning rates lead to initial learning of more specific features that do not translate well to improvements on inputs from all classes, whereas high learning rates initially benefit all classes at once. We measure stiffness as a function of distance between data points and observe that higher learning rates induce positive correlation between changes in loss further apart, pointing towards a regularization effect of learning rate. When training on CIFAR-100, the stiffness matrix exhibits a coarse-grained behavior suggestive of the model's awareness of super-class membership.