Statistical Guarantees for Estimating the Centers of a Two-component Gaussian Mixture by EM
Paper and Code
Aug 07, 2016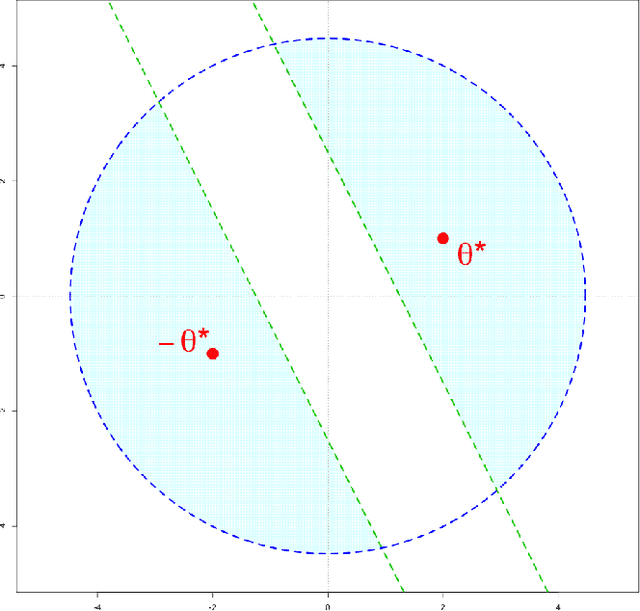
Recently, a general method for analyzing the statistical accuracy of the EM algorithm has been developed and applied to some simple latent variable models [Balakrishnan et al. 2016]. In that method, the basin of attraction for valid initialization is required to be a ball around the truth. Using Stein's Lemma, we extend these results in the case of estimating the centers of a two-component Gaussian mixture in $d$ dimensions. In particular, we significantly expand the basin of attraction to be the intersection of a half space and a ball around the origin. If the signal-to-noise ratio is at least a constant multiple of $ \sqrt{d\log d} $, we show that a random initialization strategy is feasible.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge