State space representations of the Roesser type for convolutional layers
Paper and Code
Mar 18, 2024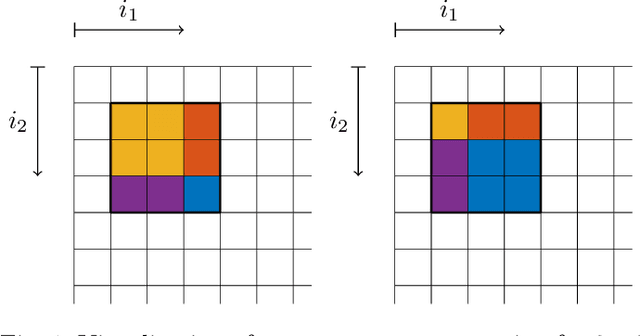
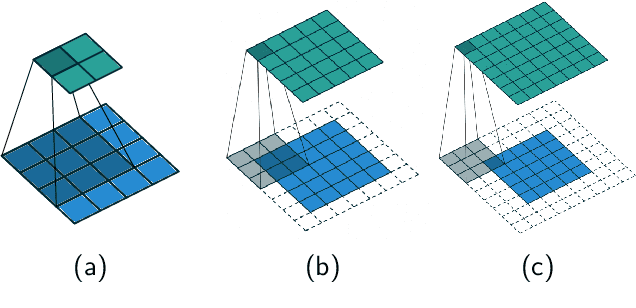
From the perspective of control theory, convolutional layers (of neural networks) are 2-D (or N-D) linear time-invariant dynamical systems. The usual representation of convolutional layers by the convolution kernel corresponds to the representation of a dynamical system by its impulse response. However, many analysis tools from control theory, e.g., involving linear matrix inequalities, require a state space representation. For this reason, we explicitly provide a state space representation of the Roesser type for 2-D convolutional layers with $c_\mathrm{in}r_1 + c_\mathrm{out}r_2$ states, where $c_\mathrm{in}$/$c_\mathrm{out}$ is the number of input/output channels of the layer and $r_1$/$r_2$ characterizes the width/length of the convolution kernel. This representation is shown to be minimal for $c_\mathrm{in} = c_\mathrm{out}$. We further construct state space representations for dilated, strided, and N-D convolutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge