Staged trees and asymmetry-labeled DAGs
Paper and Code
Aug 04, 2021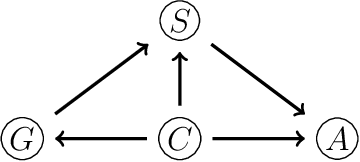
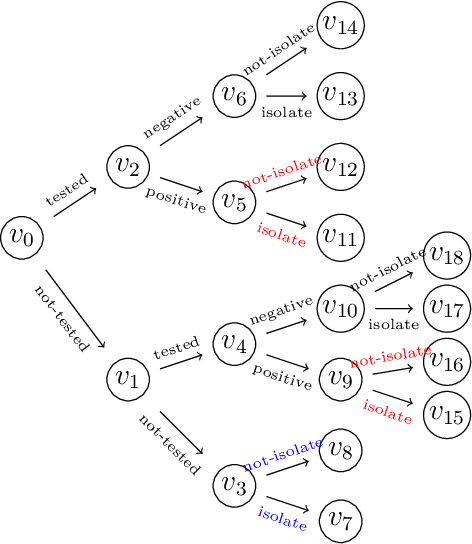
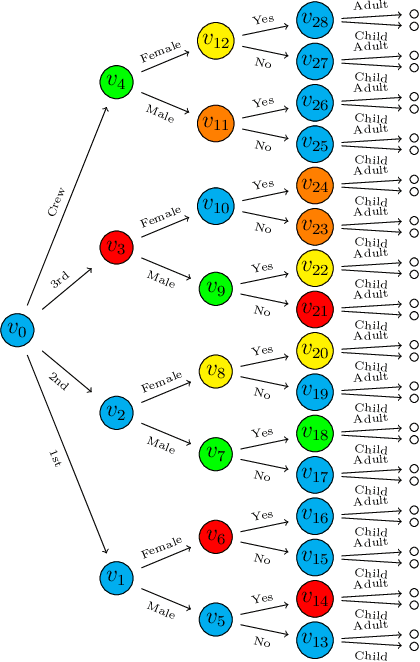
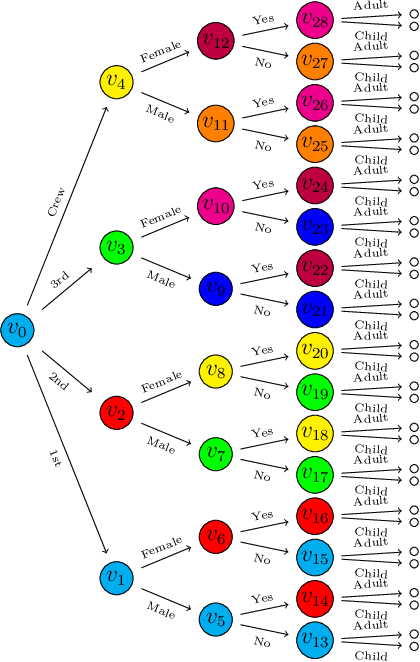
Bayesian networks are a widely-used class of probabilistic graphical models capable of representing symmetric conditional independence between variables of interest using the topology of the underlying graph. They can be seen as a special case of the much more general class of models called staged trees, which can represent any type of non-symmetric conditional independence. Here we formalize the relationship between these two models and introduce a minimal Bayesian network representation of the staged tree, which can be used to read conditional independences in an intuitive way. Furthermore, we define a new labeled graph, termed asymmetry-labeled directed acyclic graph, whose edges are labeled to denote the type of dependence existing between any two random variables. Various datasets are used to illustrate the methodology, highlighting the need to construct models which more flexibly encode and represent non-symmetric structures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge