Stability vs Implicit Bias of Gradient Methods on Separable Data and Beyond

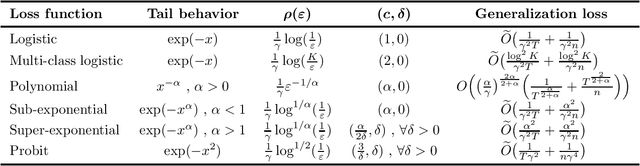
An influential line of recent work has focused on the generalization properties of unregularized gradient-based learning procedures applied to separable linear classification with exponentially-tailed loss functions. The ability of such methods to generalize well has been attributed to the their implicit bias towards large margin predictors, both asymptotically as well as in finite time. We give an additional unified explanation for this generalization and relate it to two simple properties of the optimization objective, that we refer to as realizability and self-boundedness. We introduce a general setting of unconstrained stochastic convex optimization with these properties, and analyze generalization of gradient methods through the lens of algorithmic stability. In this broader setting, we obtain sharp stability bounds for gradient descent and stochastic gradient descent which apply even for a very large number of gradient steps, and use them to derive general generalization bounds for these algorithms. Finally, as direct applications of the general bounds, we return to the setting of linear classification with separable data and establish several novel test loss and test accuracy bounds for gradient descent and stochastic gradient descent for a variety of loss functions with different tail decay rates. In some of these case, our bounds significantly improve upon the existing generalization error bounds in the literature.