Stability of Density-Based Clustering
Paper and Code
Nov 11, 2010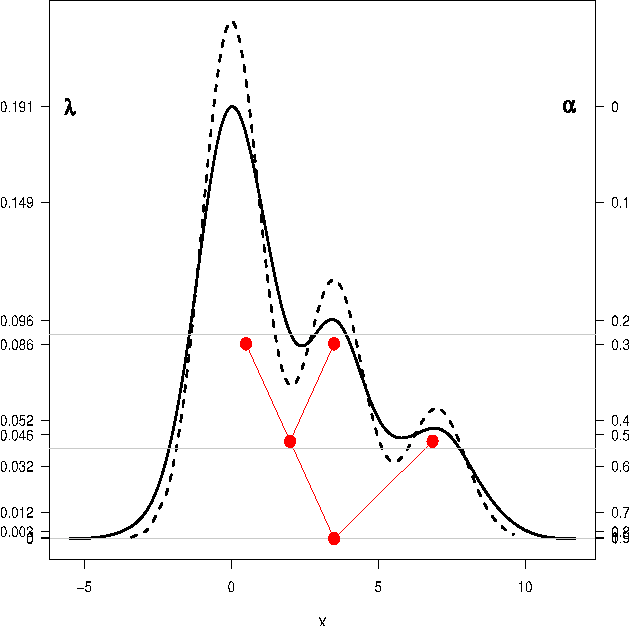
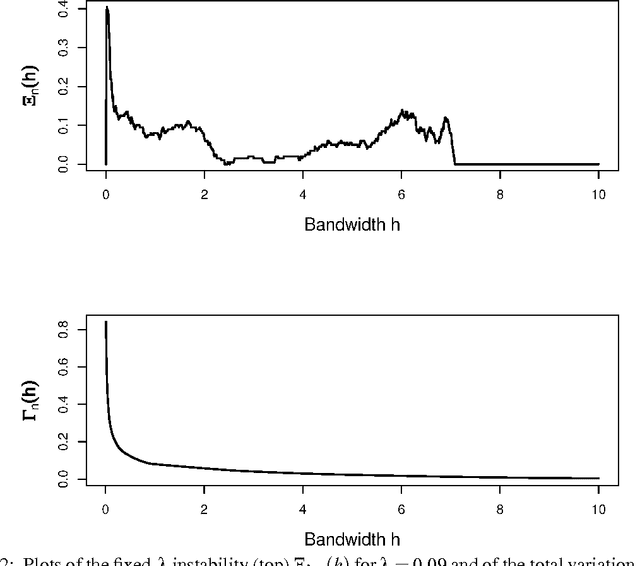
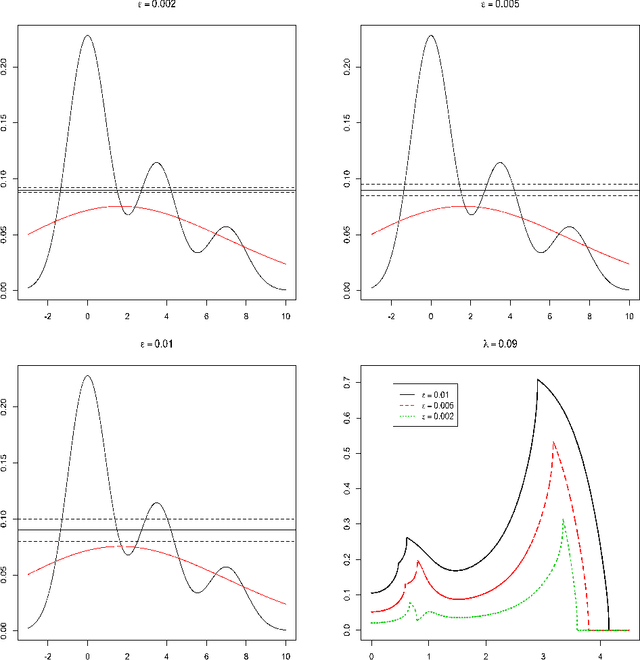
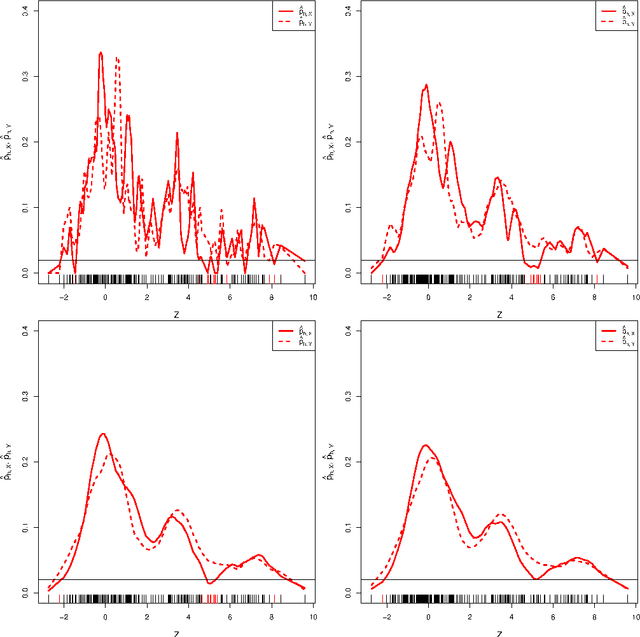
High density clusters can be characterized by the connected components of a level set $L(\lambda) = \{x:\ p(x)>\lambda\}$ of the underlying probability density function $p$ generating the data, at some appropriate level $\lambda\geq 0$. The complete hierarchical clustering can be characterized by a cluster tree ${\cal T}= \bigcup_{\lambda} L(\lambda)$. In this paper, we study the behavior of a density level set estimate $\widehat L(\lambda)$ and cluster tree estimate $\widehat{\cal{T}}$ based on a kernel density estimator with kernel bandwidth $h$. We define two notions of instability to measure the variability of $\widehat L(\lambda)$ and $\widehat{\cal{T}}$ as a function of $h$, and investigate the theoretical properties of these instability measures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge