Spurious Local Minima of Shallow ReLU Networks Conform with the Symmetry of the Target Model
Paper and Code
Dec 26, 2019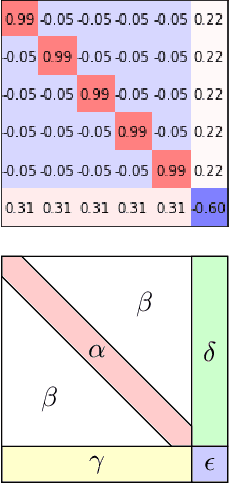
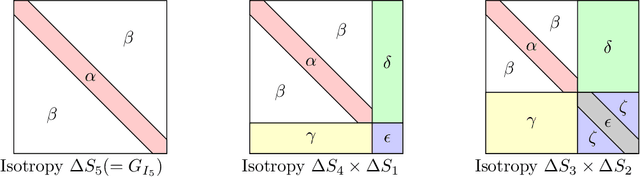
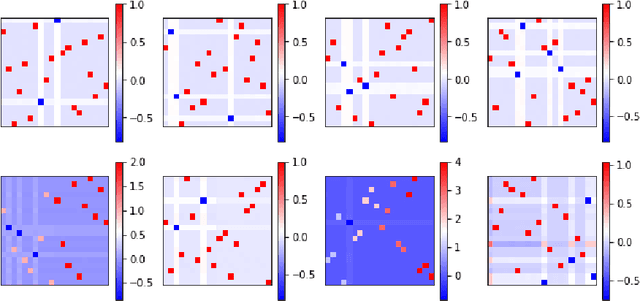

We consider the optimization problem associated with fitting two-layer ReLU networks with respect to the squared loss, where labels are assumed to be generated by a target network. Focusing first on standard Gaussian inputs, we show that the structure of spurious local minima detected by stochastic gradient descent (SGD) is, in a well-defined sense, the \emph{least loss of symmetry} with respect to the target weights. A closer look at the analysis indicates then that this principle of least symmetry breaking may apply to a broader range of settings. Motivated by this, we conduct a series of experiments which corroborate this hypothesis for different classes of non-isotropic non-product distributions, smooth activation functions and networks with a few layers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge