SPINE: Soft Piecewise Interpretable Neural Equations
Paper and Code
Nov 20, 2021
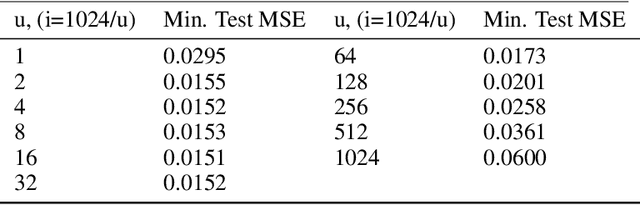
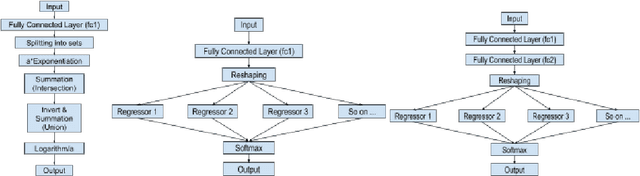

Relu Fully Connected Networks are ubiquitous but uninterpretable because they fit piecewise linear functions emerging from multi-layered structures and complex interactions of model weights. This paper takes a novel approach to piecewise fits by using set operations on individual pieces(parts). This is done by approximating canonical normal forms and using the resultant as a model. This gives special advantages like (a)strong correspondence of parameters to pieces of the fit function(High Interpretability); (b)ability to fit any combination of continuous functions as pieces of the piecewise function(Ease of Design); (c)ability to add new non-linearities in a targeted region of the domain(Targeted Learning); (d)simplicity of an equation which avoids layering. It can also be expressed in the general max-min representation of piecewise linear functions which gives theoretical ease and credibility. This architecture is tested on simulated regression and classification tasks and benchmark datasets including UCI datasets, MNIST, FMNIST, and CIFAR 10. This performance is on par with fully connected architectures. It can find a variety of applications where fully connected layers must be replaced by interpretable layers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge