Spectral Sparsification for Communication-Efficient Collaborative Rotation and Translation Estimation

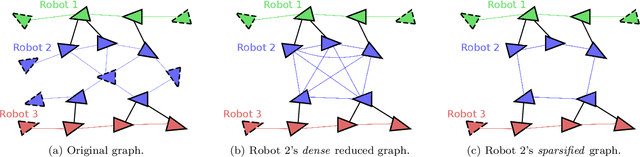
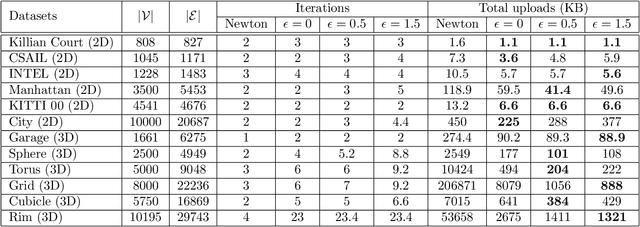
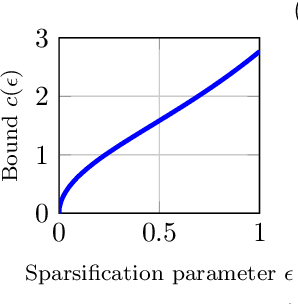
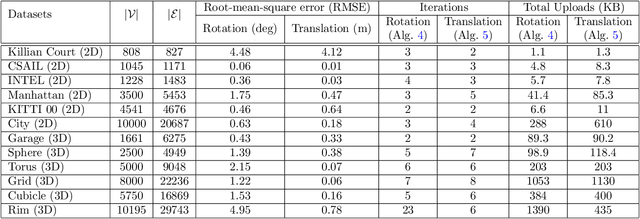
We propose fast and communication-efficient distributed algorithms for rotation averaging and translation recovery problems that arise from multi-robot simultaneous localization and mapping (SLAM) and distributed camera network localization applications. Our methods are based on theoretical relations between the Hessians of the underlying Riemannian optimization problems and the Laplacians of suitably weighted graphs. We leverage these results to design a distributed solver that performs approximate second-order optimization by solving a Laplacian system at each iteration. Crucially, our algorithms permit robots to employ spectral sparsification to sparsify intermediate dense matrices before communication, and hence provide a mechanism to trade off accuracy with communication efficiency with provable guarantees. We perform rigorous theoretical analysis of our methods and prove that they enjoy (local) linear rate of convergence on the problems of interest. Numerical experiments show that the proposed methods converge to high-precision solutions in a few iterations and that they are significantly more communication-efficient compared to baseline second-order solvers.