Spatial embedding promotes a specific form of modularity with low entropy and heterogeneous spectral dynamics
Paper and Code
Sep 26, 2024
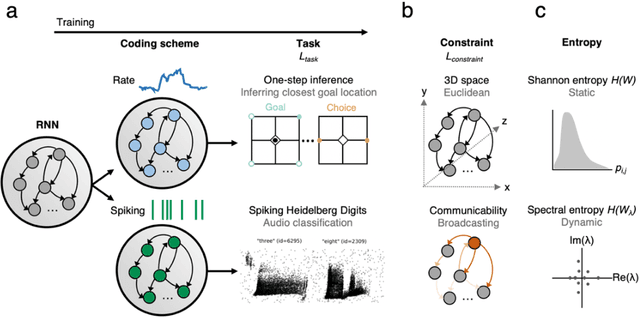
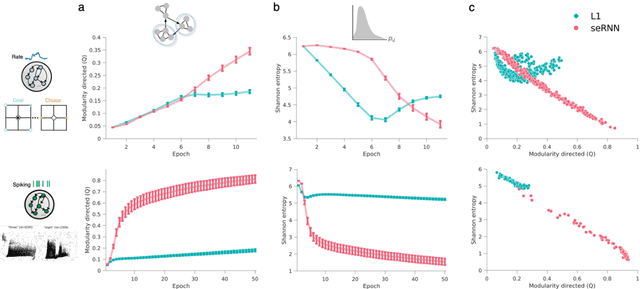
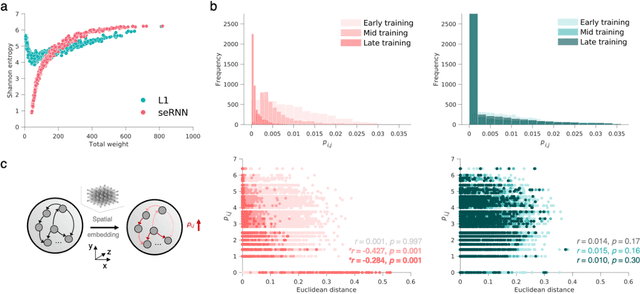
Understanding how biological constraints shape neural computation is a central goal of computational neuroscience. Spatially embedded recurrent neural networks provide a promising avenue to study how modelled constraints shape the combined structural and functional organisation of networks over learning. Prior work has shown that spatially embedded systems like this can combine structure and function into single artificial models during learning. But it remains unclear precisely how, in general, structural constraints bound the range of attainable configurations. In this work, we show that it is possible to study these restrictions through entropic measures of the neural weights and eigenspectrum, across both rate and spiking neural networks. Spatial embedding, in contrast to baseline models, leads to networks with a highly specific low entropy modularity where connectivity is readily interpretable given the known spatial and communication constraints acting on them. Crucially, these networks also demonstrate systematically modulated spectral dynamics, revealing how they exploit heterogeneity in their function to overcome the constraints imposed on their structure. This work deepens our understanding of constrained learning in neural networks, across coding schemes and tasks, where solutions to simultaneous structural and functional objectives must be accomplished in tandem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge