Sparsity-regularized coded ptychography for robust and efficient lensless microscopy on a chip
Paper and Code
Sep 24, 2023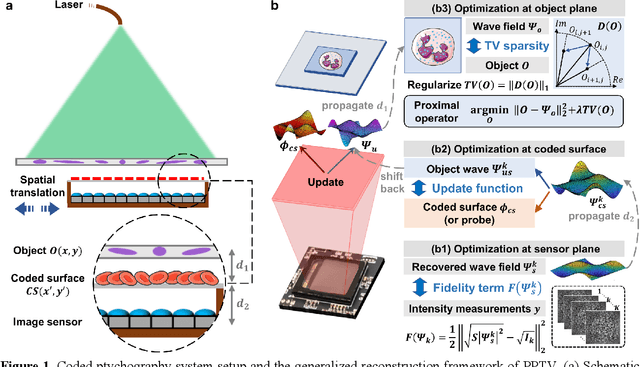

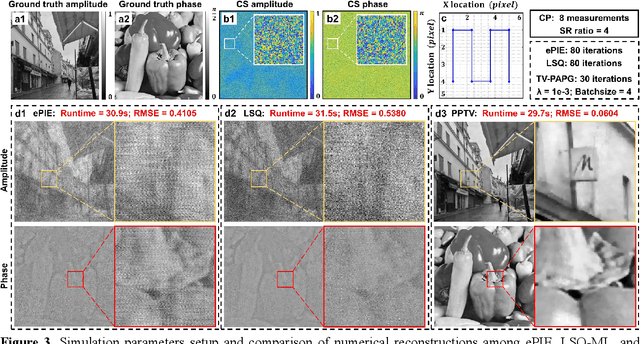

In ptychographic imaging, the trade-off between the number of acquisitions and the resultant imaging quality presents a complex optimization problem. Increasing the number of acquisitions typically yields reconstructions with higher spatial resolution and finer details. Conversely, a reduction in measurement frequency often compromises the quality of the reconstructed images, manifesting as increased noise and coarser details. To address this challenge, we employ sparsity priors to reformulate the ptychographic reconstruction task as a total variation regularized optimization problem. We introduce a new computational framework, termed the ptychographic proximal total-variation (PPTV) solver, designed to integrate into existing ptychography settings without necessitating hardware modifications. Through comprehensive numerical simulations, we validate that PPTV-driven coded ptychography is capable of producing highly accurate reconstructions with a minimal set of eight intensity measurements. Convergence analysis further substantiates the robustness, stability, and computational feasibility of the proposed PPTV algorithm. Experimental results obtained from optical setups unequivocally demonstrate that the PPTV algorithm facilitates high-throughput, high-resolution imaging while significantly reducing the measurement burden. These findings indicate that the PPTV algorithm has the potential to substantially mitigate the resource-intensive requirements traditionally associated with high-quality ptychographic imaging, thereby offering a pathway toward the development of more compact and efficient ptychographic microscopy systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge