Sparse Partitioning: Nonlinear regression with binary or tertiary predictors, with application to association studies
Paper and Code
Aug 30, 2011
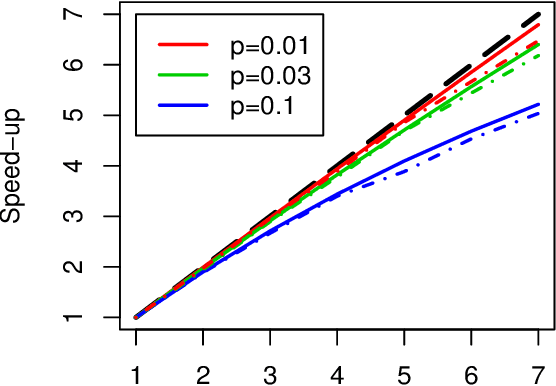
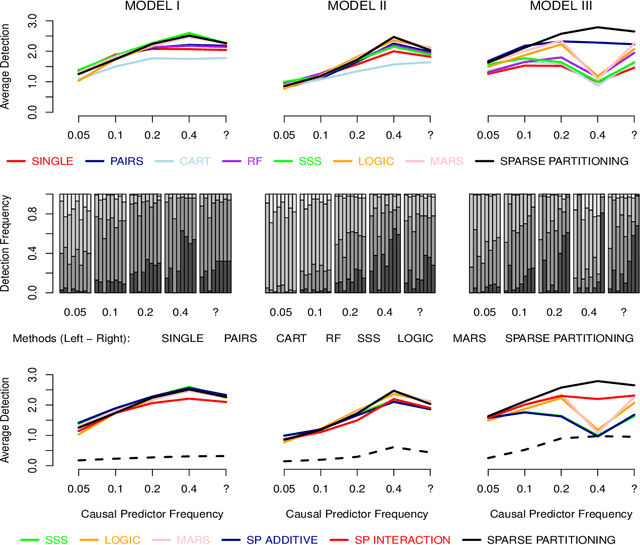
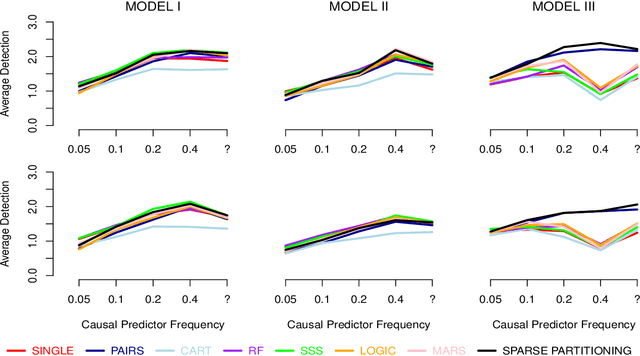
This paper presents Sparse Partitioning, a Bayesian method for identifying predictors that either individually or in combination with others affect a response variable. The method is designed for regression problems involving binary or tertiary predictors and allows the number of predictors to exceed the size of the sample, two properties which make it well suited for association studies. Sparse Partitioning differs from other regression methods by placing no restrictions on how the predictors may influence the response. To compensate for this generality, Sparse Partitioning implements a novel way of exploring the model space. It searches for high posterior probability partitions of the predictor set, where each partition defines groups of predictors that jointly influence the response. The result is a robust method that requires no prior knowledge of the true predictor--response relationship. Testing on simulated data suggests Sparse Partitioning will typically match the performance of an existing method on a data set which obeys the existing method's model assumptions. When these assumptions are violated, Sparse Partitioning will generally offer superior performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge