Sparse Gaussian Processes via Parametric Families of Compactly-supported Kernels

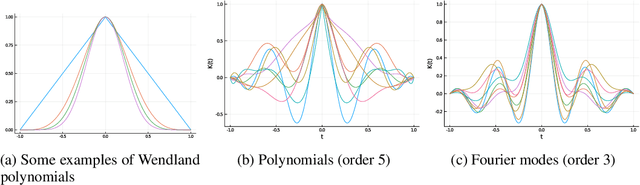
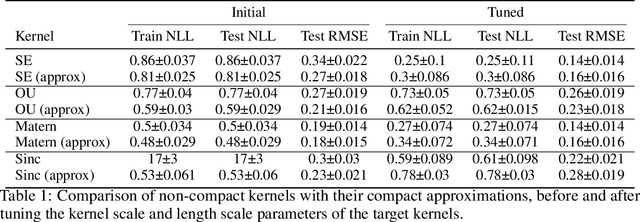
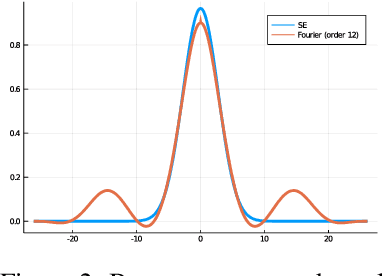
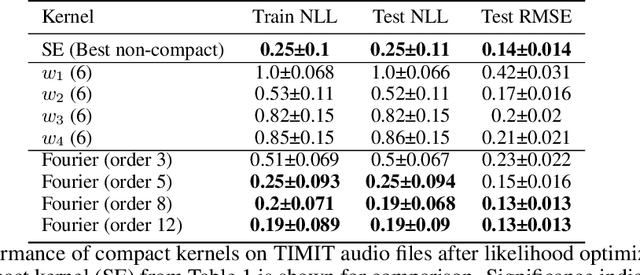
Gaussian processes are powerful models for probabilistic machine learning, but are limited in application by their $O(N^3)$ inference complexity. We propose a method for deriving parametric families of kernel functions with compact spatial support, which yield naturally sparse kernel matrices and enable fast Gaussian process inference via sparse linear algebra. These families generalize known compactly-supported kernel functions, such as the Wendland polynomials. The parameters of this family of kernels can be learned from data using maximum likelihood estimation. Alternatively, we can quickly compute compact approximations of a target kernel using convex optimization. We demonstrate that these approximations incur minimal error over the exact models when modeling data drawn directly from a target GP, and can out-perform the traditional GP kernels on real-world signal reconstruction tasks, while exhibiting sub-quadratic inference complexity.