Solving Bayesian Network Structure Learning Problem with Integer Linear Programming
Paper and Code
Jul 06, 2020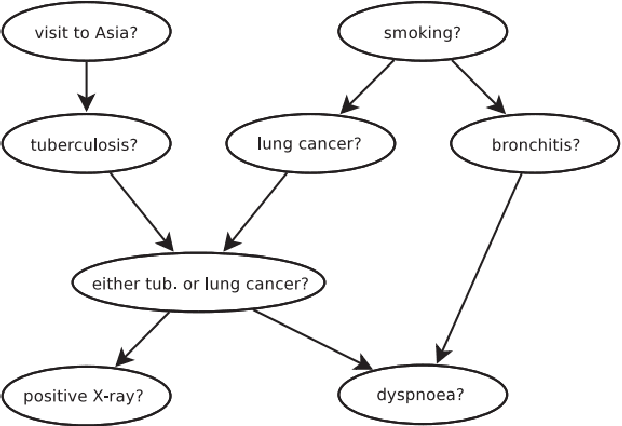
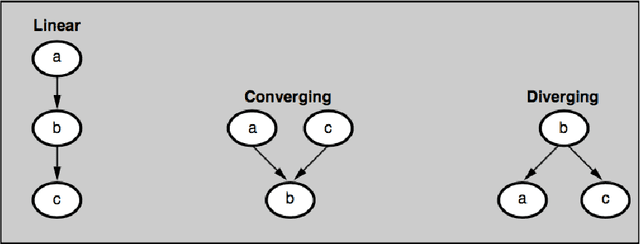
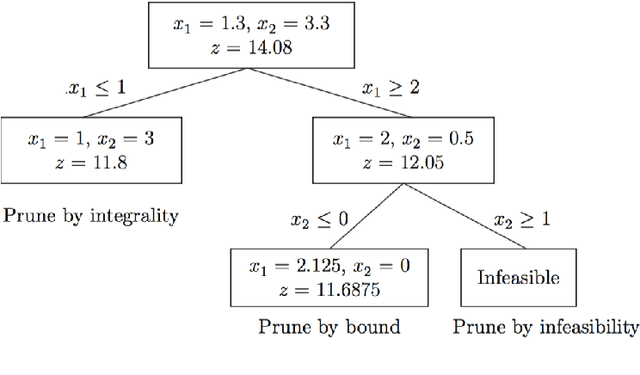
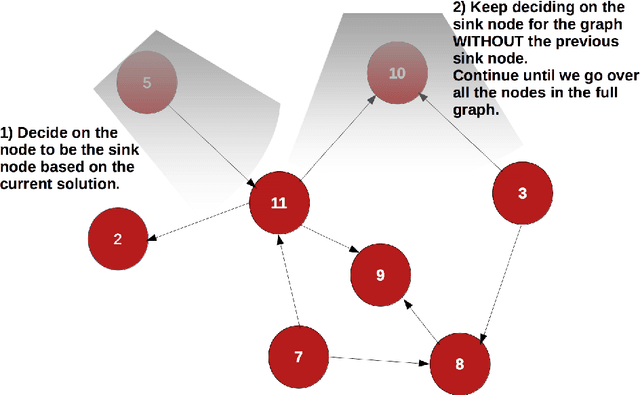
This dissertation investigates integer linear programming (ILP) formulation of Bayesian Network structure learning problem. We review the definition and key properties of Bayesian network and explain score metrics used to measure how well certain Bayesian network structure fits the dataset. We outline the integer linear programming formulation based on the decomposability of score metrics. In order to ensure acyclicity of the structure, we add ``cluster constraints'' developed specifically for Bayesian network, in addition to cycle constraints applicable to directed acyclic graphs in general. Since there would be exponential number of these constraints if we specify them fully, we explain the methods to add them as cutting planes without declaring them all in the initial model. Also, we develop a heuristic algorithm that finds a feasible solution based on the idea of sink node on directed acyclic graphs. We implemented the ILP formulation and cutting planes as a \textsf{Python} package, and present the results of experiments with different settings on reference datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge