Solve-Select-Scale: A Three Step Process For Sparse Signal Estimation
Paper and Code
May 16, 2016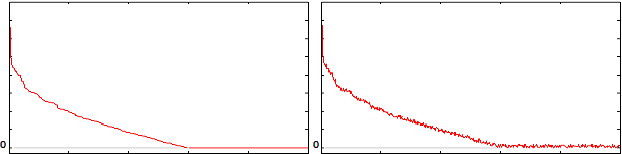
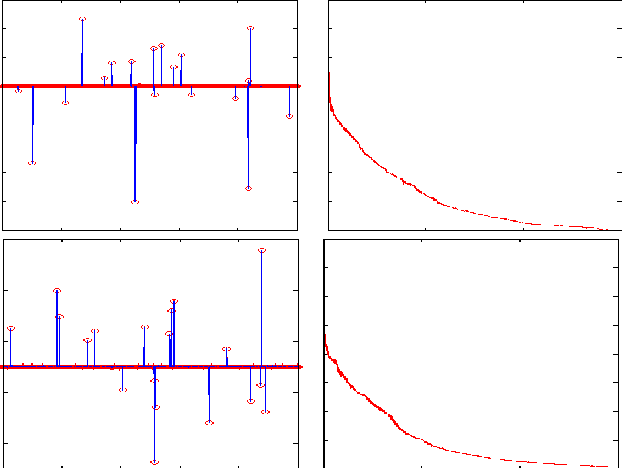
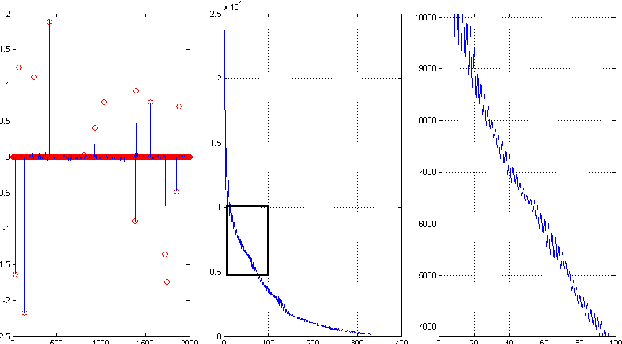
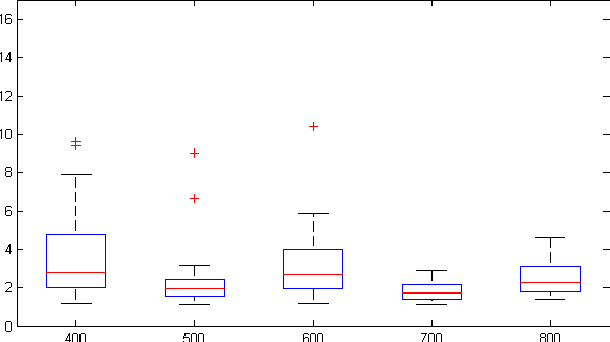
In the theory of compressed sensing (CS), the sparsity $\|x\|_0$ of the unknown signal $\mathbf{x} \in \mathcal{R}^n$ is of prime importance and the focus of reconstruction algorithms has mainly been either $\|x\|_0$ or its convex relaxation (via $\|x\|_1$). However, it is typically unknown in practice and has remained a challenge when nothing about the size of the support is known. As pointed recently, $\|x\|_0$ might not be the best metric to minimize directly, both due to its inherent complexity as well as its noise performance. Recently a novel stable measure of sparsity $s(\mathbf{x}) := \|\mathbf{x}\|_1^2/\|\mathbf{x}\|_2^2$ has been investigated by Lopes \cite{Lopes2012}, which is a sharp lower bound on $\|\mathbf{x}\|_0$. The estimation procedure for this measure uses only a small number of linear measurements, does not rely on any sparsity assumptions, and requires very little computation. The usage of the quantity $s(\mathbf{x})$ in sparse signal estimation problems has not received much importance yet. We develop the idea of incorporating $s(\mathbf{x})$ into the signal estimation framework. We also provide a three step algorithm to solve problems of the form $\mathbf{Ax=b}$ with no additional assumptions on the original signal $\mathbf{x}$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge