Software Implementation of the Krylov Methods Based Reconstruction for the 3D Cone Beam CT Operator
Paper and Code
Oct 26, 2021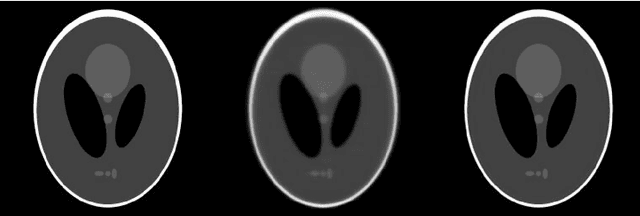
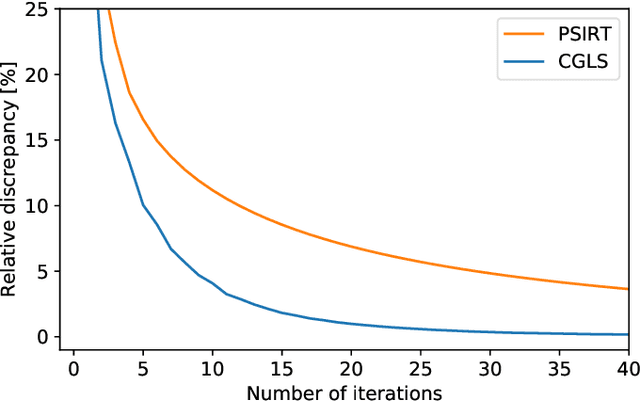
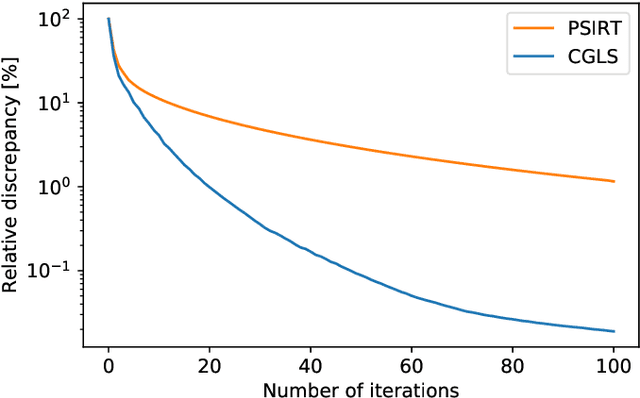
Krylov subspace methods are considered a standard tool to solve large systems of linear algebraic equations in many scientific disciplines such as image restoration or solving partial differential equations in mechanics of continuum. In the context of computer tomography however, the mostly used algebraic reconstruction techniques are based on classical iterative schemes. In this work we present software package that implements fully 3D cone beam projection operator and uses Krylov subspace methods, namely CGLS and LSQR to solve related tomographic reconstruction problems. It also implements basic preconditioning strategies. On the example of the cone beam CT reconstruction of 3D Shepp-Logan phantom we show that the speed of convergence of the CGLS clearly outperforms PSIRT algorithm. Therefore Krylov subspace methods present an interesting option for the reconstruction of large 3D cone beam CT problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge