Soft Hoeffding Tree: A Transparent and Differentiable Model on Data Streams
Paper and Code
Nov 07, 2024
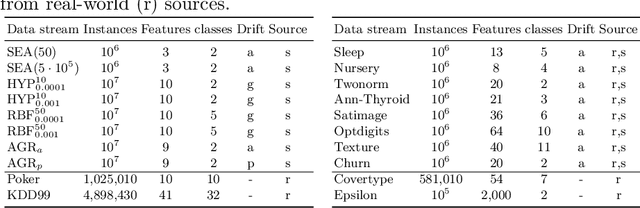


We propose soft Hoeffding trees (SoHoT) as a new differentiable and transparent model for possibly infinite and changing data streams. Stream mining algorithms such as Hoeffding trees grow based on the incoming data stream, but they currently lack the adaptability of end-to-end deep learning systems. End-to-end learning can be desirable if a feature representation is learned by a neural network and used in a tree, or if the outputs of trees are further processed in a deep learning model or workflow. Different from Hoeffding trees, soft trees can be integrated into such systems due to their differentiability, but are neither transparent nor explainable. Our novel model combines the extensibility and transparency of Hoeffding trees with the differentiability of soft trees. We introduce a new gating function to regulate the balance between univariate and multivariate splits in the tree. Experiments are performed on 20 data streams, comparing SoHoT to standard Hoeffding trees, Hoeffding trees with limited complexity, and soft trees applying a sparse activation function for sample routing. The results show that soft Hoeffding trees outperform Hoeffding trees in estimating class probabilities and, at the same time, maintain transparency compared to soft trees, with relatively small losses in terms of AUROC and cross-entropy. We also demonstrate how to trade off transparency against performance using a hyperparameter, obtaining univariate splits at one end of the spectrum and multivariate splits at the other.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge