Sketching for Principal Component Regression
Paper and Code
Mar 07, 2018
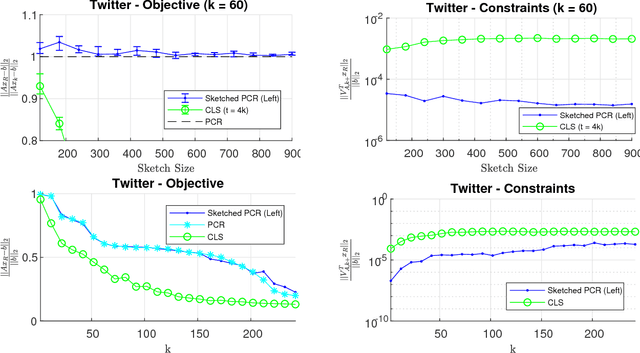
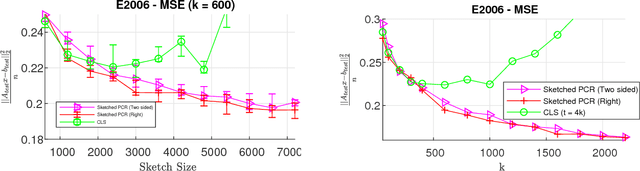
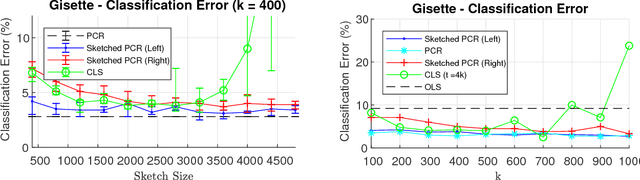
Principal component regression (PCR) is a useful method for regularizing linear regression. Although conceptually simple, straightforward implementations of PCR have high computational costs and so are inappropriate when learning with large scale data. In this paper, we propose efficient algorithms for computing approximate PCR solutions that are, on one hand, high quality approximations to the true PCR solutions (when viewed as minimizer of a constrained optimization problem), and on the other hand entertain rigorous risk bounds (when viewed as statistical estimators). In particular, we propose an input sparsity time algorithms for approximate PCR. We also consider computing an approximate PCR in the streaming model, and kernel PCR. Empirical results demonstrate the excellent performance of our proposed methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge