Skeleton Extraction from 3D Point Clouds by Decomposing the Object into Parts
Paper and Code
Dec 26, 2019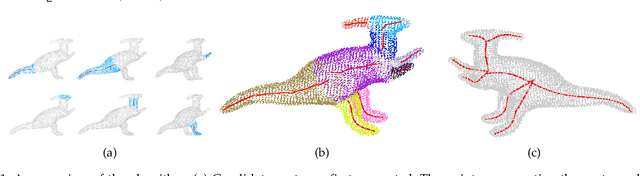
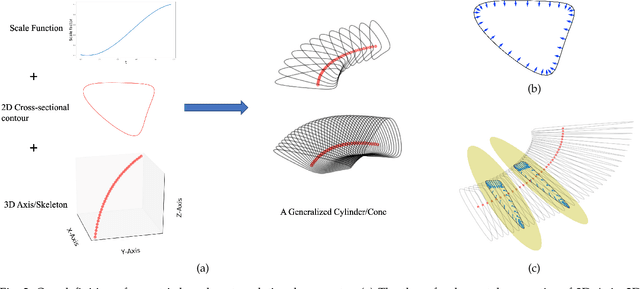

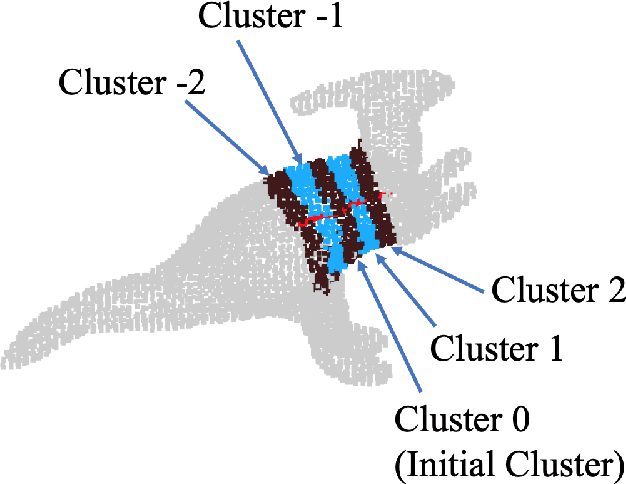
Decomposing a point cloud into its components and extracting curve skeletons from point clouds are two related problems. Decomposition of a shape into its components is often obtained as a byproduct of skeleton extraction. In this work, we propose to extract curve skeletons, from unorganized point clouds, by decomposing the object into its parts, identifying part skeletons and then linking these part skeletons together to obtain the complete skeleton. We believe it is the most natural way to extract skeletons in the sense that this would be the way a human would approach the problem. Our parts are generalized cylinders (GCs). Since, the axis of a GC is an integral part of its definition, the parts have natural skeletal representations. We use translational symmetry, the fundamental property of GCs, to extract parts from point clouds. We demonstrate how this method can handle a large variety of shapes. We compare our method with state of the art methods and show how a part based approach can deal with some of the limitations of other methods. We present an improved version of an existing point set registration algorithm and demonstrate its utility in extracting parts from point clouds. We also show how this method can be used to extract skeletons from and identify parts of noisy point clouds. A part based approach also provides a natural and intuitive interface for user interaction. We demonstrate the ease with which mistakes, if any, can be fixed with minimal user interaction with the help of a graphical user interface.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge