Single Memristor Logic Gates: From NOT to a Full Adder
Paper and Code
Oct 19, 2015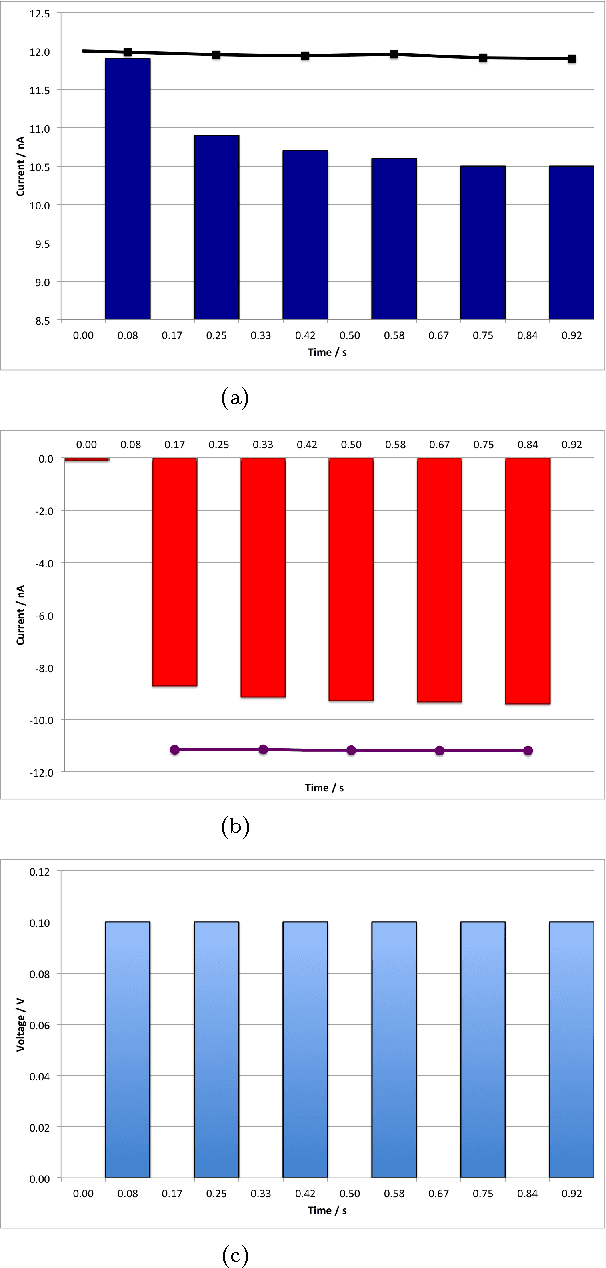

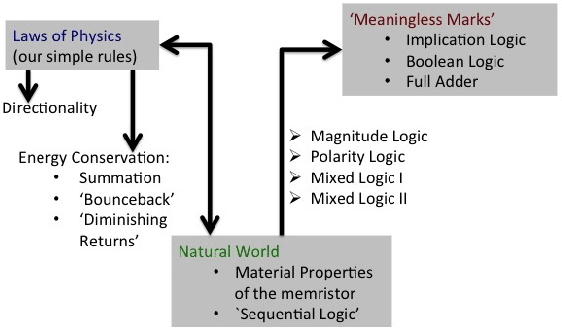
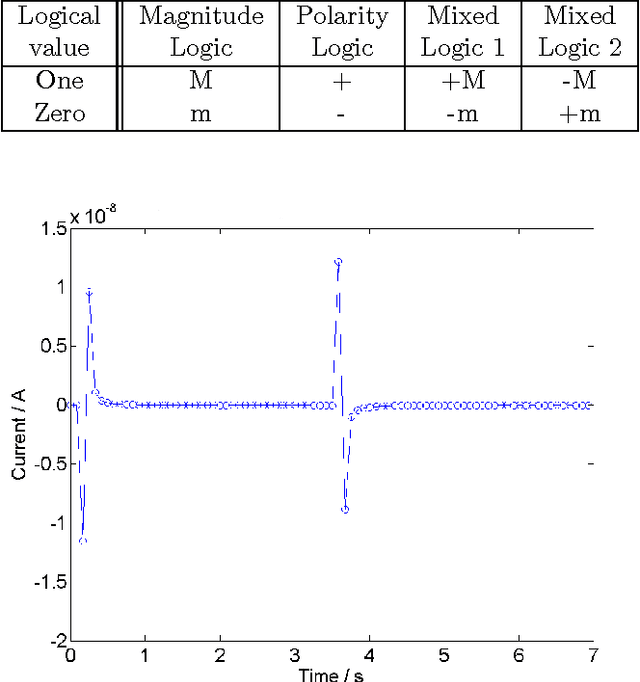
Memristors have been suggested as a novel route to neuromorphic computing based on the similarity between them and neurons (specifically synapses and ion pumps). The d.c. action of the memristor is a current spike which imparts a short-term memory to the device. Here it is demonstrated that this short-term memory works exactly like habituation (e.g. in \emph{Aplysia}). We elucidate the physical rules, based on energy conservation, governing the interaction of these current spikes: summation, `bounce-back', directionality and `diminishing returns'. Using these rules, we introduce 4 different logical systems to implement sequential logic in the memristor and demonstrate how sequential logic works by instantiating a NOT gate, an AND gate, an XOR gate and a Full Adder with a single memristor. The Full Adder makes use of the memristor's short-term memory to add together three binary values and outputs the sum, the carry digit and even the order they were input in. A memristor full adder also outputs the arithmetical sum of bits, allowing for a logically (but not physically) reversible system. Essentially, we can replace an input/output port with an extra time-step, allowing a single memristor to do a hither-to unexpectedly large amount of computation. This makes up for the memristor's slow operation speed and may relate to how neurons do a similarly-large computation with such slow operations speeds. We propose that using spiking logic, either in gates or as neuron-analogues, with plastic rewritable connections between them, would allow the building of a neuromorphic computer.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge