Simulated annealing for weighted polygon packing
Paper and Code
Sep 29, 2008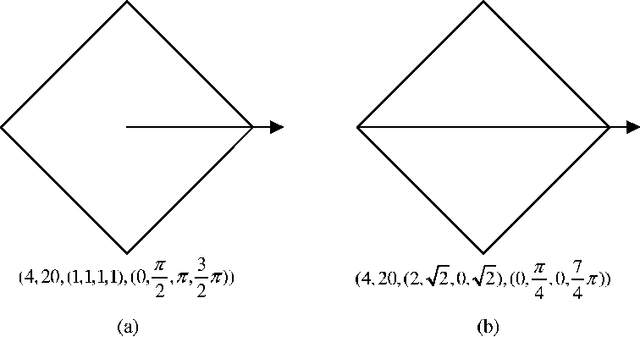
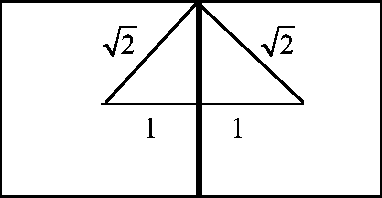
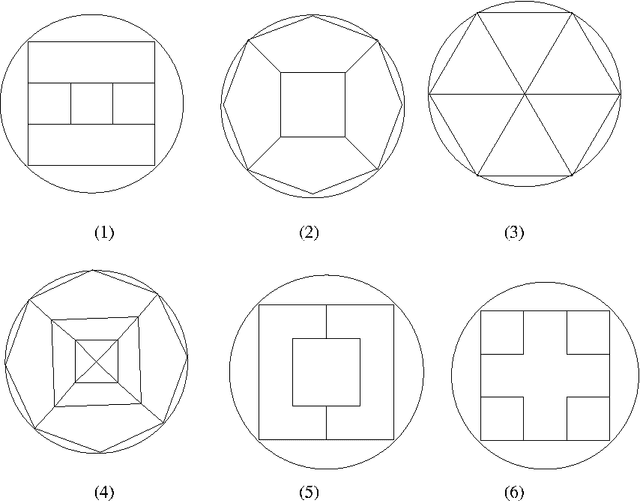
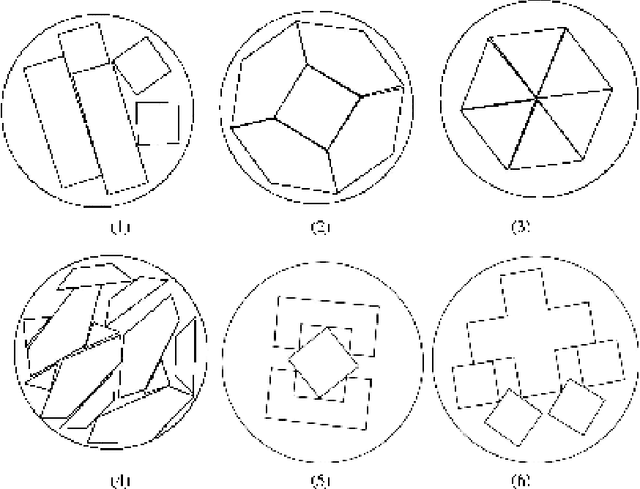
In this paper we present a new algorithm for a layout optimization problem: this concerns the placement of weighted polygons inside a circular container, the two objectives being to minimize imbalance of mass and to minimize the radius of the container. This problem carries real practical significance in industrial applications (such as the design of satellites), as well as being of significant theoretical interest. Previous work has dealt with circular or rectangular objects, but here we deal with the more realistic case where objects may be represented as polygons and the polygons are allowed to rotate. We present a solution based on simulated annealing and first test it on instances with known optima. Our results show that the algorithm obtains container radii that are close to optimal. We also compare our method with existing algorithms for the (special) rectangular case. Experimental results show that our approach out-performs these methods in terms of solution quality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge