SILVar: Single Index Latent Variable Models
Paper and Code
Mar 24, 2018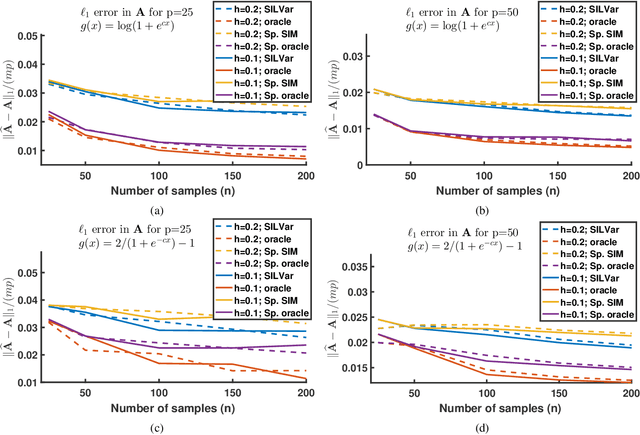
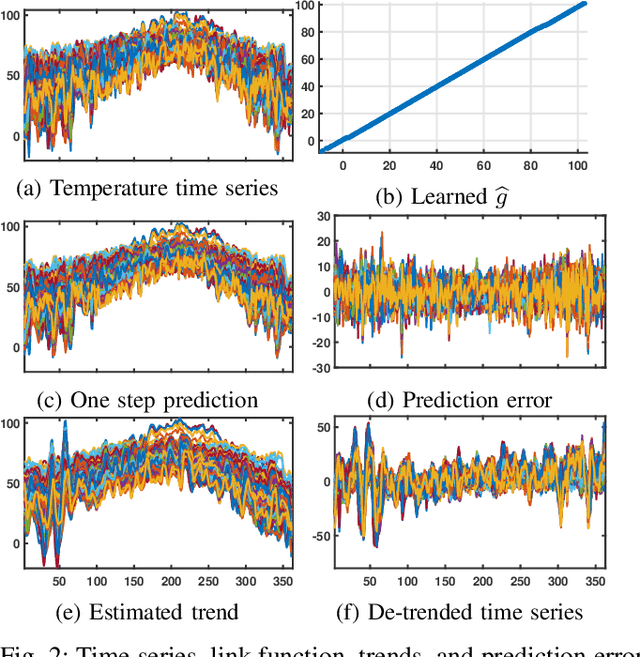
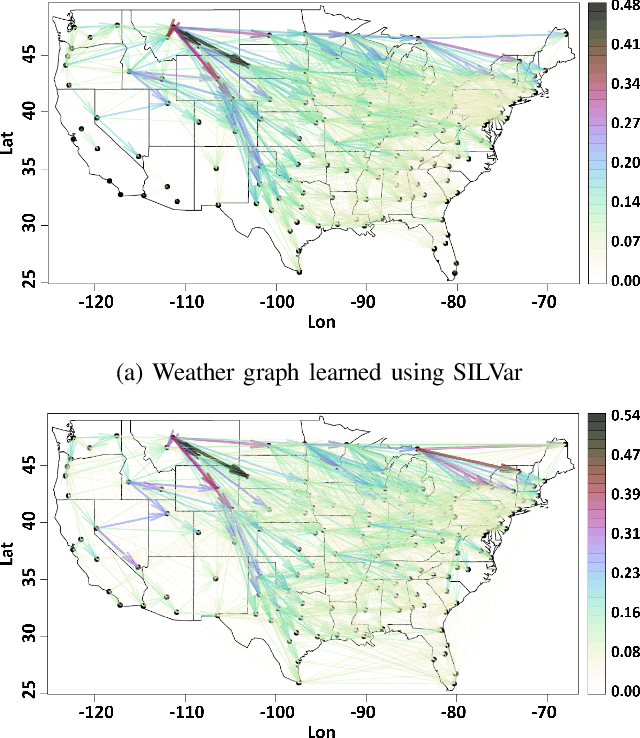

A semi-parametric, non-linear regression model in the presence of latent variables is introduced. These latent variables can correspond to unmodeled phenomena or unmeasured agents in a complex networked system. This new formulation allows joint estimation of certain non-linearities in the system, the direct interactions between measured variables, and the effects of unmodeled elements on the observed system. The particular form of the model adopted is justified, and learning is posed as a regularized empirical risk minimization. This leads to classes of structured convex optimization problems with a "sparse plus low-rank" flavor. Relations between the proposed model and several common model paradigms, such as those of Robust Principal Component Analysis (PCA) and Vector Autoregression (VAR), are established. Particularly in the VAR setting, the low-rank contributions can come from broad trends exhibited in the time series. Details of the algorithm for learning the model are presented. Experiments demonstrate the performance of the model and the estimation algorithm on simulated and real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge