Sheaf Hypergraph Networks
Paper and Code
Sep 29, 2023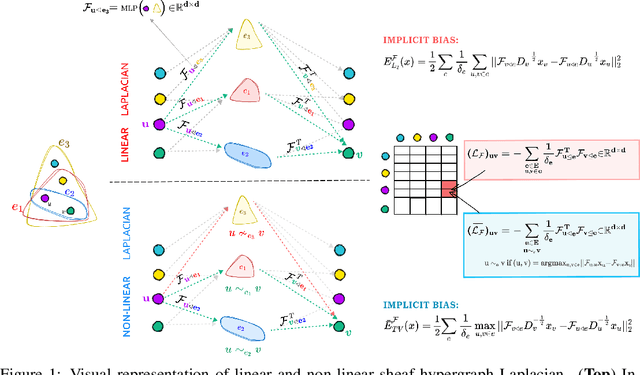
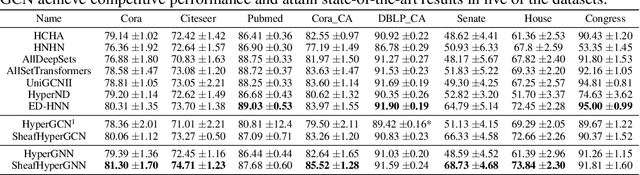

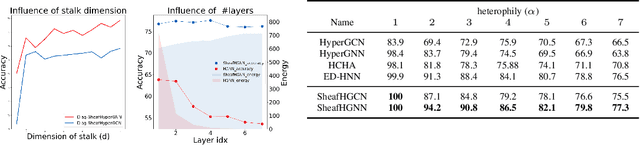
Higher-order relations are widespread in nature, with numerous phenomena involving complex interactions that extend beyond simple pairwise connections. As a result, advancements in higher-order processing can accelerate the growth of various fields requiring structured data. Current approaches typically represent these interactions using hypergraphs. We enhance this representation by introducing cellular sheaves for hypergraphs, a mathematical construction that adds extra structure to the conventional hypergraph while maintaining their local, higherorder connectivity. Drawing inspiration from existing Laplacians in the literature, we develop two unique formulations of sheaf hypergraph Laplacians: linear and non-linear. Our theoretical analysis demonstrates that incorporating sheaves into the hypergraph Laplacian provides a more expressive inductive bias than standard hypergraph diffusion, creating a powerful instrument for effectively modelling complex data structures. We employ these sheaf hypergraph Laplacians to design two categories of models: Sheaf Hypergraph Neural Networks and Sheaf Hypergraph Convolutional Networks. These models generalize classical Hypergraph Networks often found in the literature. Through extensive experimentation, we show that this generalization significantly improves performance, achieving top results on multiple benchmark datasets for hypergraph node classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge