Shapley-based explainability on the data manifold
Paper and Code
Jun 01, 2020

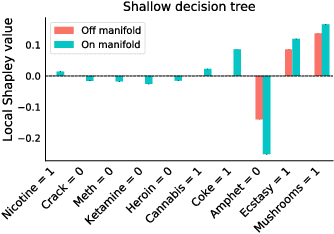
Explainability in machine learning is crucial for iterative model development, compliance with regulation, and providing operational nuance to model predictions. Shapley values provide a general framework for explainability by attributing a model's output prediction to its input features in a mathematically principled and model-agnostic way. However, practical implementations of the Shapley framework make an untenable assumption: that the model's input features are uncorrelated. In this work, we articulate the dangers of this assumption and introduce two solutions for computing Shapley explanations that respect the data manifold. One solution, based on generative modelling, provides flexible access to on-manifold data imputations, while the other directly learns the Shapley value function in a supervised way, providing performance and stability at the cost of flexibility. While the commonly used ``off-manifold'' Shapley values can (i) break symmetries in the data, (ii) give rise to misleading wrong-sign explanations, and (iii) lead to uninterpretable explanations in high-dimensional data, our approach to on-manifold explainability demonstrably overcomes each of these problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge