Shallow Encoder Deep Decoder (SEDD) Networks for Image Encryption and Decryption
Paper and Code
Jan 09, 2020
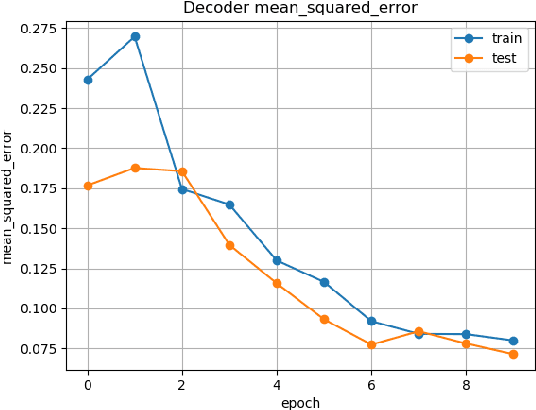

This paper explores a new framework for lossy image encryption and decryption using a simple shallow encoder neural network E for encryption, and a complex deep decoder neural network D for decryption. E is kept simple so that encoding can be done on low power and portable devices and can in principle be any nonlinear function which outputs an encoded vector. D is trained to decode the encodings using the dataset of image - encoded vector pairs obtained from E and happens independently of E. As the encodings come from E which while being a simple neural network, still has thousands of random parameters and therefore the encodings would be practically impossible to crack without D. This approach differs from autoencoders as D is trained completely independently of E, although the structure may seem similar. Therefore, this paper also explores empirically if a deep neural network can learn to reconstruct the original data in any useful form given the output of a neural network or any other nonlinear function, which can have very useful applications in Cryptanalysis. Experiments demonstrate the potential of the framework through qualitative and quantitative evaluation of the decoded images from D along with some limitations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge