Sequential Training of Neural Networks with Gradient Boosting

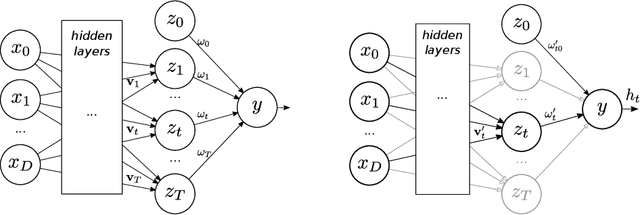
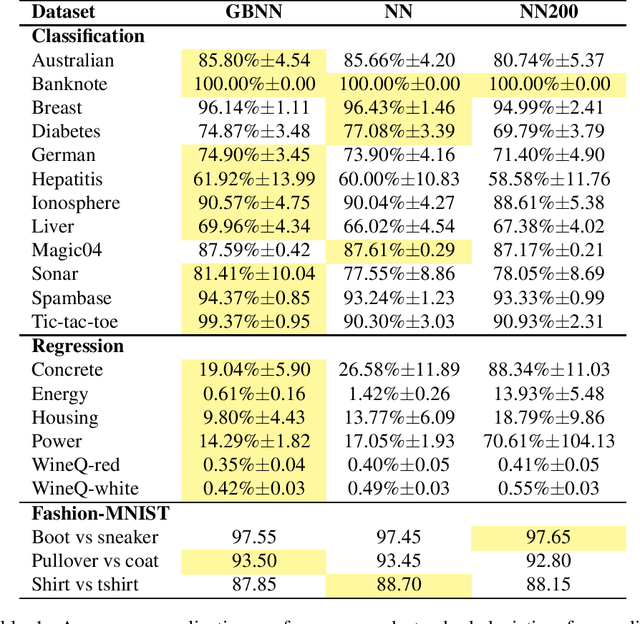
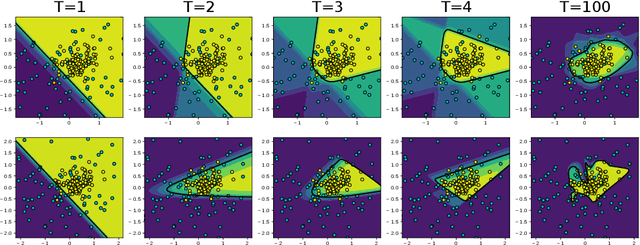
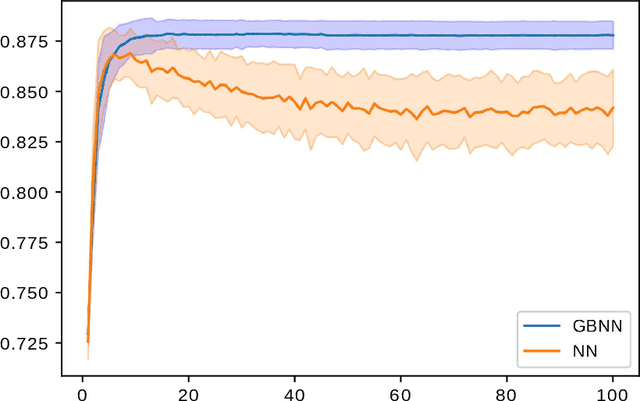
This paper presents a novel technique based on gradient boosting to train a shallow neural network (NN). Gradient boosting is an additive expansion algorithm in which a series of models are trained sequentially to approximate a given function. A one hidden layer neural network can also be seen as an additive model where the scalar product of the responses of the hidden layer and its weights provide the final output of the network. Instead of training the network as a whole, the proposed algorithm trains the network sequentially in $T$ steps. First, the bias term of the network is initialized with a constant approximation that minimizes the average loss of the data. Then, at each step, a portion of the network, composed of $K$ neurons, is trained to approximate the pseudo-residuals on the training data computed from the previous iteration. Finally, the $T$ partial models and bias are integrated as a single NN with $T \times K$ neurons in the hidden layer. We show that the proposed algorithm is more robust to overfitting than a standard neural network with respect to the number of neurons of the last hidden layer. Furthermore, we show that the proposed method design permits to reduce the number of neurons to be used without a significant reduction of its generalization ability. This permits to adapt the model to different classification speed requirements on the fly. Extensive experiments in classification and regression tasks, as well as in combination with a deep convolutional neural network, are carried out showing a better generalization performance than a standard neural network.