Semiparametric energy-based probabilistic models
Paper and Code
May 24, 2016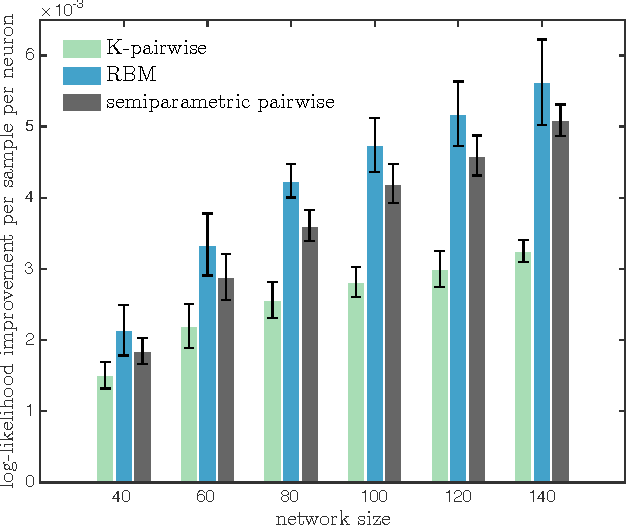
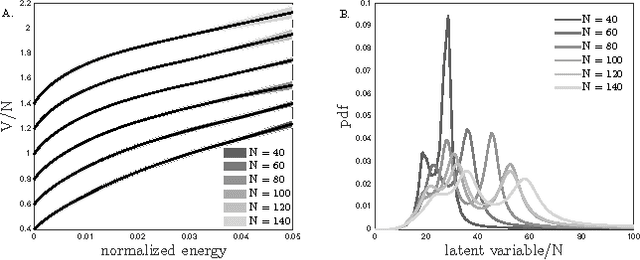
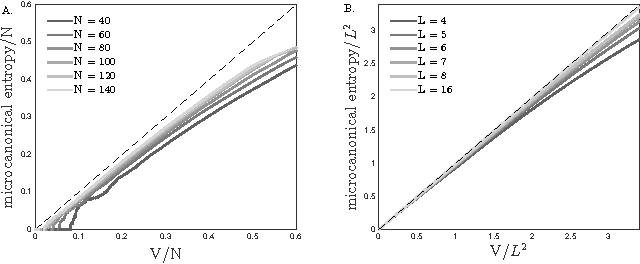
Probabilistic models can be defined by an energy function, where the probability of each state is proportional to the exponential of the state's negative energy. This paper considers a generalization of energy-based models in which the probability of a state is proportional to an arbitrary positive, strictly decreasing, and twice differentiable function of the state's energy. The precise shape of the nonlinear map from energies to unnormalized probabilities has to be learned from data together with the parameters of the energy function. As a case study we show that the above generalization of a fully visible Boltzmann machine yields an accurate model of neural activity of retinal ganglion cells. We attribute this success to the model's ability to easily capture distributions whose probabilities span a large dynamic range, a possible consequence of latent variables that globally couple the system. Similar features have recently been observed in many datasets, suggesting that our new method has wide applicability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge