Semiblind subgraph reconstruction in Gaussian graphical models
Paper and Code
Nov 15, 2017
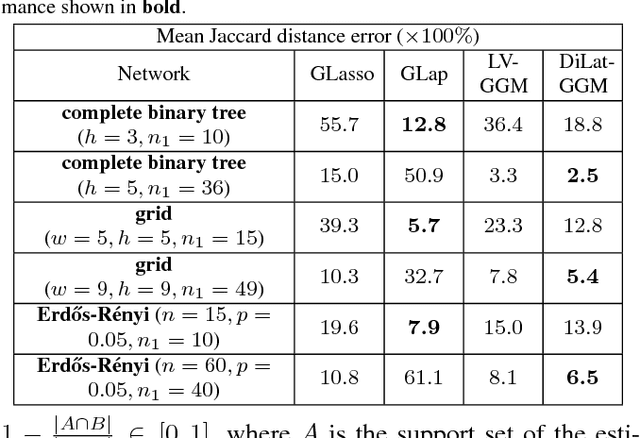

Consider a social network where only a few nodes (agents) have meaningful interactions in the sense that the conditional dependency graph over node attribute variables (behaviors) is sparse. A company that can only observe the interactions between its own customers will generally not be able to accurately estimate its customers' dependency subgraph: it is blinded to any external interactions of its customers and this blindness creates false edges in its subgraph. In this paper we address the semiblind scenario where the company has access to a noisy summary of the complementary subgraph connecting external agents, e.g., provided by a consolidator. The proposed framework applies to other applications as well, including field estimation from a network of awake and sleeping sensors and privacy-constrained information sharing over social subnetworks. We propose a penalized likelihood approach in the context of a graph signal obeying a Gaussian graphical models (GGM). We use a convex-concave iterative optimization algorithm to maximize the penalized likelihood.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge