Semi-supervised learning for structured regression on partially observed attributed graphs
Paper and Code
Mar 28, 2018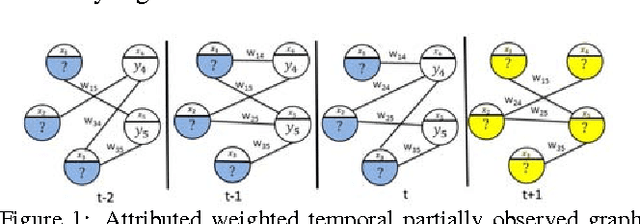
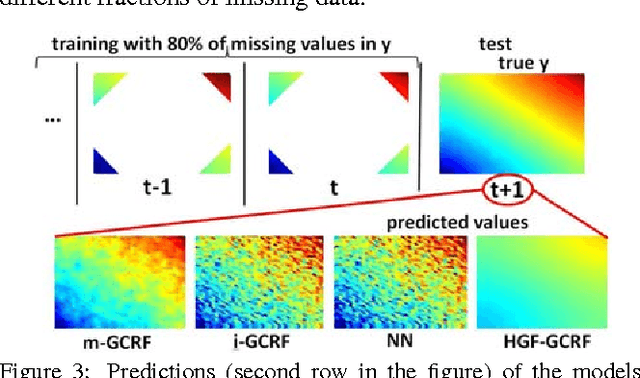
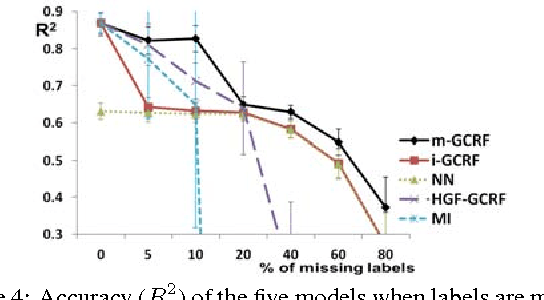
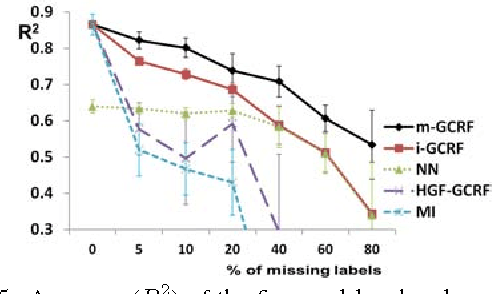
Conditional probabilistic graphical models provide a powerful framework for structured regression in spatio-temporal datasets with complex correlation patterns. However, in real-life applications a large fraction of observations is often missing, which can severely limit the representational power of these models. In this paper we propose a Marginalized Gaussian Conditional Random Fields (m-GCRF) structured regression model for dealing with missing labels in partially observed temporal attributed graphs. This method is aimed at learning with both labeled and unlabeled parts and effectively predicting future values in a graph. The method is even capable of learning from nodes for which the response variable is never observed in history, which poses problems for many state-of-the-art models that can handle missing data. The proposed model is characterized for various missingness mechanisms on 500 synthetic graphs. The benefits of the new method are also demonstrated on a challenging application for predicting precipitation based on partial observations of climate variables in a temporal graph that spans the entire continental US. We also show that the method can be useful for optimizing the costs of data collection in climate applications via active reduction of the number of weather stations to consider. In experiments on these real-world and synthetic datasets we show that the proposed model is consistently more accurate than alternative semi-supervised structured models, as well as models that either use imputation to deal with missing values or simply ignore them altogether.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge