Self-Triggered Markov Decision Processes
Paper and Code
Feb 17, 2021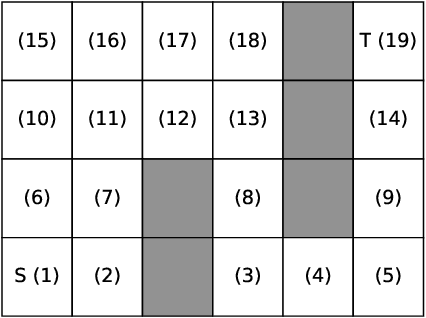
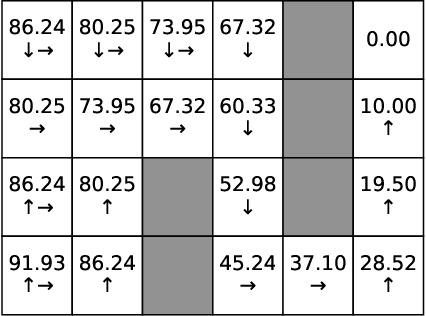
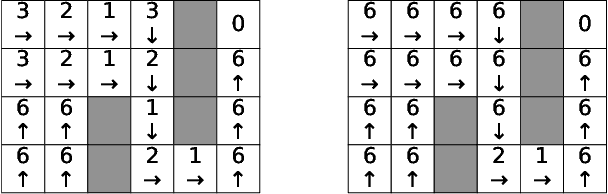
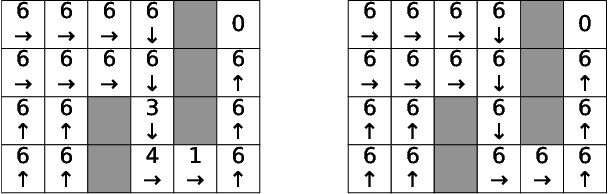
In this paper, we study Markov Decision Processes (MDPs) with self-triggered strategies, where the idea of self-triggered control is extended to more generic MDP models. This extension broadens the application of self-triggering policies to a broader range of systems. We study the co-design problems of the control policy and the triggering policy to optimize two pre-specified cost criteria. The first cost criterion is introduced by incorporating a pre-specified update penalty into the traditional MDP cost criteria to reduce the use of communication resources. Under this criteria, a novel dynamic programming (DP) equation called DP equation with optimized lookahead to proposed to solve for the self-triggering policy under this criteria. The second self-triggering policy is to maximize the triggering time while still guaranteeing a pre-specified level of sub-optimality. Theoretical underpinnings are established for the computation and implementation of both policies. Through a gridworld numerical example, we illustrate the two policies' effectiveness in reducing sources consumption and demonstrate the trade-offs between resource consumption and system performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge