Self-Supervised Hybrid Inference in State-Space Models
Paper and Code
Jul 28, 2021
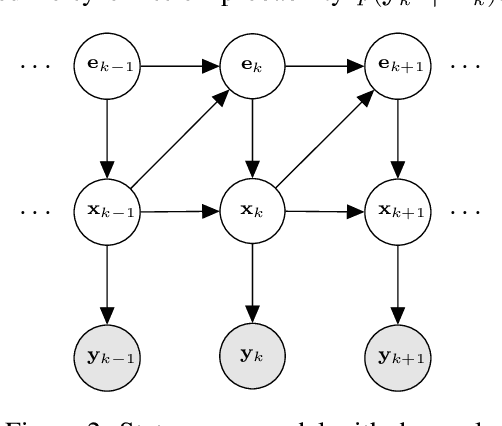

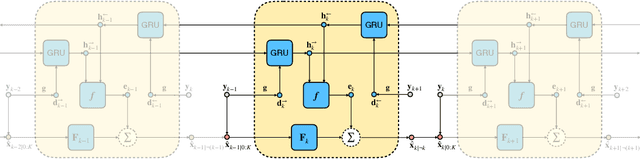
We perform approximate inference in state-space models that allow for nonlinear higher-order Markov chains in latent space. The conditional independencies of the generative model enable us to parameterize only an inference model, which learns to estimate clean states in a self-supervised manner using maximum likelihood. First, we propose a recurrent method that is trained directly on noisy observations. Afterward, we cast the model such that the optimization problem leads to an update scheme that backpropagates through a recursion similar to the classical Kalman filter and smoother. In scientific applications, domain knowledge can give a linear approximation of the latent transition maps. We can easily incorporate this knowledge into our model, leading to a hybrid inference approach. In contrast to other methods, experiments show that the hybrid method makes the inferred latent states physically more interpretable and accurate, especially in low-data regimes. Furthermore, we do not rely on an additional parameterization of the generative model or supervision via uncorrupted observations or ground truth latent states. Despite our model's simplicity, we obtain competitive results on the chaotic Lorenz system compared to a fully supervised approach and outperform a method based on variational inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge