Self-Satisfied: An end-to-end framework for SAT generation and prediction
Paper and Code
Oct 18, 2024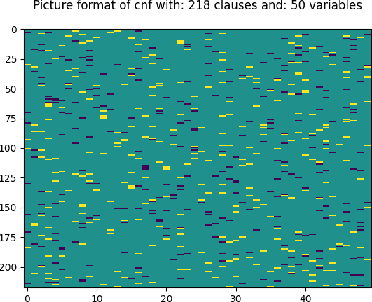

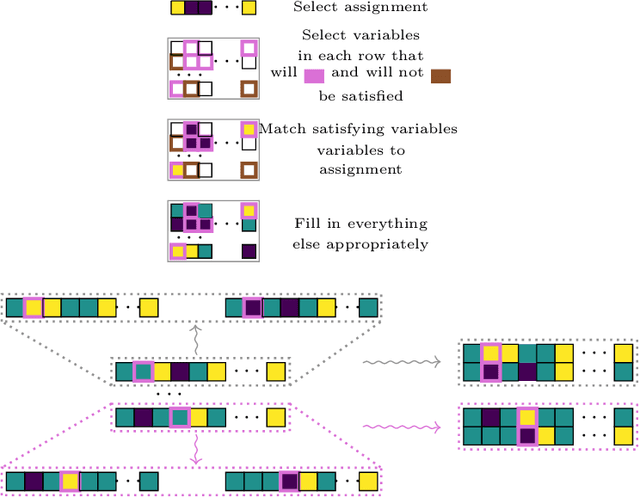
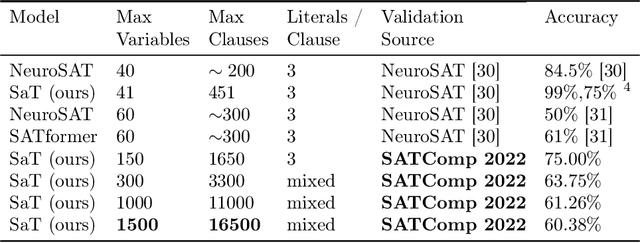
The boolean satisfiability (SAT) problem asks whether there exists an assignment of boolean values to the variables of an arbitrary boolean formula making the formula evaluate to True. It is well-known that all NP-problems can be coded as SAT problems and therefore SAT is important both practically and theoretically. From both of these perspectives, better understanding the patterns and structure implicit in SAT data is of significant value. In this paper, we describe several advances that we believe will help open the door to such understanding: we introduce hardware accelerated algorithms for fast SAT problem generation, a geometric SAT encoding that enables the use of transformer architectures typically applied to vision tasks, and a simple yet effective technique we term head slicing for reducing sequence length representation inside transformer architectures. These advances allow us to scale our approach to SAT problems with thousands of variables and tens of thousands of clauses. We validate our architecture, termed Satisfiability Transformer (SaT), on the SAT prediction task with data from the SAT Competition (SATComp) 2022 problem sets. Prior related work either leveraged a pure machine learning approach, but could not handle SATComp-sized problems, or was hybrid in the sense of integrating a machine learning component in a standard SAT solving tool. Our pure machine learning approach achieves prediction accuracies comparable to recent work, but on problems that are an order of magnitude larger than previously demonstrated. A fundamental aspect of our work concerns the very nature of SAT data and its suitability for training machine learning models. We both describe experimental results that probe the landscape of where SAT data can be successfully used for learning and position these results within the broader context of complexity and learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge