Self-learning sparse PCA for multimode process monitoring
Paper and Code
Aug 07, 2021

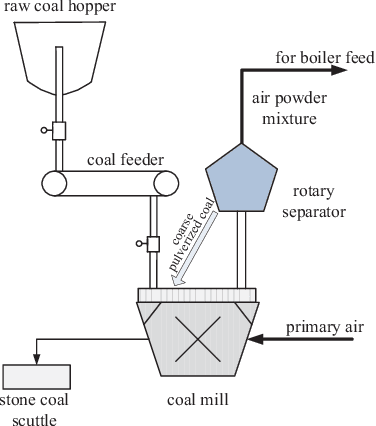
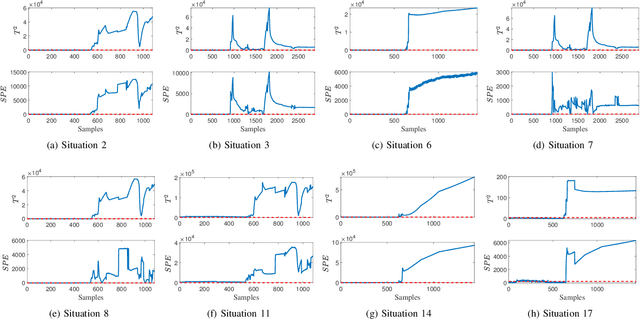
This paper proposes a novel sparse principal component analysis algorithm with self-learning ability for successive modes, where synaptic intelligence is employed to measure the importance of variables and a regularization term is added to preserve the learned knowledge of previous modes. Different from traditional multimode monitoring methods, the monitoring model is updated based on the current model and new data when a new mode arrives, thus delivering prominent performance for sequential modes. Besides, the computation and storage resources are saved in the long run, because it is not necessary to retrain the model from scratch frequently and store data from previous modes. More importantly, the model furnishes excellent interpretability owing to the sparsity of parameters. Finally, a numerical case and a practical pulverizing system are adopted to illustrate the effectiveness of the proposed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge