Selective Inference for Sparse Multitask Regression with Applications in Neuroimaging
Paper and Code
May 27, 2022
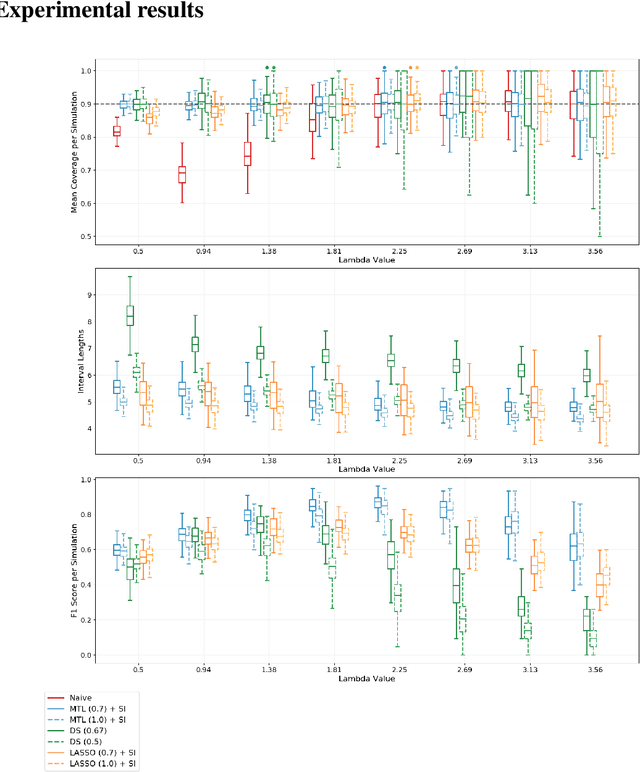
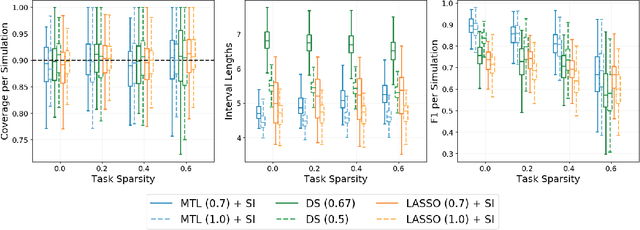
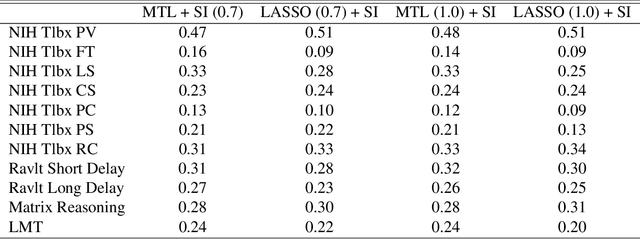
Multi-task learning is frequently used to model a set of related response variables from the same set of features, improving predictive performance and modeling accuracy relative to methods that handle each response variable separately. Despite the potential of multi-task learning to yield more powerful inference than single-task alternatives, prior work in this area has largely omitted uncertainty quantification. Our focus in this paper is a common multi-task problem in neuroimaging, where the goal is to understand the relationship between multiple cognitive task scores (or other subject-level assessments) and brain connectome data collected from imaging. We propose a framework for selective inference to address this problem, with the flexibility to: (i) jointly identify the relevant covariates for each task through a sparsity-inducing penalty, and (ii) conduct valid inference in a model based on the estimated sparsity structure. Our framework offers a new conditional procedure for inference, based on a refinement of the selection event that yields a tractable selection-adjusted likelihood. This gives an approximate system of estimating equations for maximum likelihood inference, solvable via a single convex optimization problem, and enables us to efficiently form confidence intervals with approximately the correct coverage. Applied to both simulated data and data from the Adolescent Cognitive Brain Development (ABCD) study, our selective inference methods yield tighter confidence intervals than commonly used alternatives, such as data splitting. We also demonstrate through simulations that multi-task learning with selective inference can more accurately recover true signals than single-task methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge