Selection of the Most Probable Best
Paper and Code
Jul 15, 2022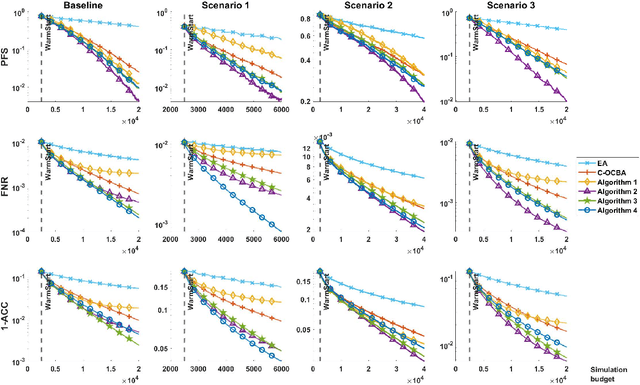

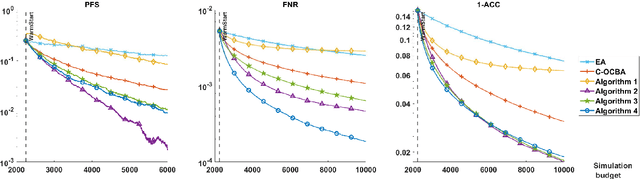
We consider an expected-value ranking and selection problem where all k solutions' simulation outputs depend on a common uncertain input model. Given that the uncertainty of the input model is captured by a probability simplex on a finite support, we define the most probable best (MPB) to be the solution whose probability of being optimal is the largest. To devise an efficient sampling algorithm to find the MPB, we first derive a lower bound to the large deviation rate of the probability of falsely selecting the MPB, then formulate an optimal computing budget allocation (OCBA) problem to find the optimal static sampling ratios for all solution-input model pairs that maximize the lower bound. We devise a series of sequential algorithms that apply interpretable and computationally efficient sampling rules and prove their sampling ratios achieve the optimality conditions for the OCBA problem as the simulation budget increases. The algorithms are benchmarked against a state-of-the-art sequential sampling algorithm designed for contextual ranking and selection problems and demonstrated to have superior empirical performances at finding the MPB.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge